Ce code fait partie de la famille des codes à 2 dimensions, il peut encoder jusqu'à 2335 caractères sur une
très petite surface.L'encodage se fait en deux étapes : tout d'abord les données sont converties en
"mots-clé" de 8 bits. (Encodage de haut niveau) puis ceux-ci sont convertis en petits carrés noirs et blancs.
(Encodage de bas niveau) De plus un système de correction des erreurs permet de reconstituer des données mal
imprimées, effacées, floues ou arrachées. Dans la suite de cet exposé, l'expression "mot-clé" sera abrégée
en MC et "code de Reed-Solomon" en RS.
La structure générale.
-
Le symbole est une zone carrée ou rectangulaire constituée de lignes
et colonnes. Chaque cellule est un petit carré noir pour un bit à 1 et blanc
pour un bit à 0. La dimension du carré est appelée le module.
- Les couleurs peuvent être interverties : blanc sur noir.
-
Le protocole ECI (Extended Channel Interpretation) procure un mode pour spécifier une interprétation
particulière des valeurs des octets ou pour identifier une page de code particulière.
Par défaut le
code ECI est 000003 qui désigne l'alphabet Latin ISO 8859-1.
-
Il y a deux standards datamatrix : ECC 000-140 et ECC 200. Seul
l'ECC 200 peux être utilisé pour un nouveau projet. Cette étude ne porte que sur l'ECC 200.
-
Un symbole consiste en une ou plusieurs régions de données. Chaque
région à une bordure épaisse d'un module.
-
Independamment du nombre de région, il y a une, et une seule, matrice. La taille de la matrice est :
"dimension de la région" x "nombre de région"
Exemple pour le symbole 36x36 : "16x16" x "2x2"
---> la taille de la matrice est 32x32
Second exemple pour le symbole 16x48 : "14x22" x "1x2" ---> la taille de la matrice est 14x44
- Le nombre de lignes et le nombre de colonnes (incluant la bordure) sont toujours pairs (Impairs pour ECC 000-140 !)
- Si necessaire un mécanisme permet de répartir plus de données sur plusieurs symboles. (Jusqu'à 16)
- Le mécanisme de correction des erreurs est basé sur les codes de Reed-Solomon.
-
Pour les symboles carrés de 48 x 48 et moins, les codes de Reed-Solomon sont ajoutés après les
données ; pour les autres symboles ils sont entrelaçés : les données sont divisées en blocs.
- Chaque taille de symbole a son propre nombre de codes de Reed-Solomon.
- Le nombre total de MC par symbole est égal au nombre de cellules de la matrice divisé par 8 (Sans partie décimale)
-
Les 8 bits de chaque MC sont placés dans la matrice de gauche à droite
et de haut en bas, certains MC sont scindés afin de remplir la matrice.
- Une marge d'au moins 1 module de large est requise sur les 4 cotés.
-
Attention à ne pas confondre la notion de région (qui
est une division graphique du symbole) et la notion de blocs qui est une division logique des données.
Un code de 2 x 2 régions :
L'encodage de bas niveau.
-
On utilisera par la suite les opérateurs : + --> addition, x --> multiplication,
\ --> division entière, MOD --> reste de la division entière.
-
Il existe 24 tailles de symbole carré et 6 tailles de symbole
rectangulaire. Le tableau suivant donne les valeurs de base pour chaque taille de symbole.
Taille du symbole
Lignes x colonnes
|
Nombre de
région de données
(H x V)
|
Nombre de MC de
Reed Solomon
|
Nombre de
blocs
|
|
Symboles carrés
|
| 10x10 |
1 |
5 |
1 |
| 12x12 |
1 |
7 |
1 |
| 14x14 |
1 |
10 |
1 |
| 16x16 |
1 |
12 |
1 |
| 18x18 |
1 |
14 |
1 |
| 20x20 |
1 |
18 |
1 |
| 22x22 |
1 |
20 |
1 |
| 24x24 |
1 |
24 |
1 |
| 26x26 |
1 |
28 |
1 |
| 32x32 |
2x2 |
36 |
1 |
| 36x36 |
2x2 |
42 |
1 |
| 40x40 |
2x2 |
48 |
1 |
| 44x44 |
2x2 |
56 |
1 |
| 48x48 |
2x2 |
68 |
1 |
| 52x52 |
2x2 |
2 x 42 |
2 |
| 64x64 |
4x4 |
2 x 56 |
2 |
| 72x72 |
4x4 |
4 x 36 |
4 |
| 80x80 |
4x4 |
4 x 48 |
4 |
| 88x88 |
4x4 |
4 x 56 |
4 |
| 96x96 |
4x4 |
4 x 68 |
4 |
| 104x104 |
4x4 |
6 x 56 |
6 |
| 120x120 |
6x6 |
6 x 68 |
6 |
| 132x132 |
6x6 |
8 x 62 |
8 |
| 144x144 |
6x6 |
10 x 62 |
8 |
|
Symboles rectangulaires |
| 8x18 |
1 |
7 |
1 |
| 8x32 |
2 |
11 |
1 |
| 12x26 |
1 |
14 |
1 |
| 12x36 |
1x2 |
18 |
1 |
| 16x36 |
1x2 |
24 |
1 |
| 16x48 |
1x2 |
28 |
1 |
-
D'autres valeurs intéressantes peuvent être calculées à partir de
celles-ci. Cela est fait à l'aide d'une feuille de calcul :
-
Chaque région a une bordure épaisse de un module. Les cotés gauches et inférieurs sont entièrement
noirs, les cotés droits et supérieurs sont fait d'une alternance de carrés noirs et blancs.
-
Chaque MC est placé dans la matrice (S'il y a plusieurs régions, elles sont
assemblées pour former une matrice unique) selon des lignes parallèles à 45 degrés
et le coin supérieur gauche est toujours comme montré ci-dessous :
Sur
cette image nous remarquons que les MC 2, 5 et 6 ont une forme régulière. Les
MC 1, 3, 4 sont tronqués et le reste de ces MC est reporté de l'autre coté
du symbole. Voici la disposition complète d'une matrice de 8 x 8 :
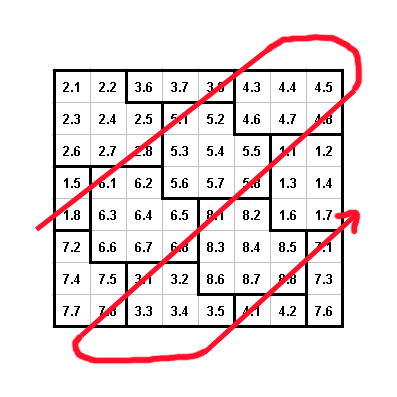Vous pouvez remarquer sur cette image que le bit 8 de chaque MC est sous l'une
des lignes parallèles à 45 degrés. Les conditions de coin et de bordure
sont très complexes et différentes pour chaque taille de matrice. Heureusement
le standard Datamatrix nous donne un algorithme pour réaliser le placement.
L'encodage de haut biveau.
-
L'encodage de haut niveau supporte 6 modes de compression, le mode
ASCII se divise en 3 sous modes :
| Mode de compression |
Données à encoder |
Taux de compression |
| ASCII |
Caractères ASCII 0 à 127 |
1 octet par MC |
| ASCII étendu |
Caractères ASCII 128 à 255 |
0.5 octet par MC |
| ASCII numerique |
Chiffres ASCII |
2 octets par MC |
| C40 |
Majuscules alphanumeriques |
1.5 octet par MC |
| TEXT |
Minuscules alphanumeriques |
1.5 octet par MC |
| X12 |
ANSI X12 |
1.5 octet par MC |
| EDIFACT |
Caractères ASCII 32 à 94 |
1.33 octet par MC |
| BASE 256 |
Caractères ASCII 0 à 255 |
1 octet par MC |
-
Le mode d'encodage par défaut est le mode ASCII. Des MCs spéciaux
permettent de basculer d'un mode d'encodage à un autre.
| Mot-clés |
Donnée ou fonction |
| 1 Ã 128 |
Données ASCII |
| 129 |
Remplissage |
| 130 Ã 229 |
Paire de chiffres : 00 Ã 99 |
| 230 |
Commute vers le mode C40 |
| 231 |
Commute vers le mode Base 256 |
| 232 |
Ccaractère FNC1 |
| 233 |
Structure de symboles multiples |
| 234 |
Programmation du lecteur |
| 235 |
Passage en ASCII étendu pour un caractère |
| 236 |
Macro |
| 237 |
Macro |
| 238 |
Commute vers le mode ANSI X12 |
| 239 |
Commute vers le mode TEXT |
| 240 |
Commute vers le mode EDIFACT |
| 241 |
Caractère E.C.I. |
| 254 |
Si le mode ASCII est en cours :
Fin des données, les MCs suivant sont des MCs de remplissage
Si un autre mode est en cours :
Commute vers le mode ASCII ou indique la fin des données
|
-
Si le symbole n'est pas plein, des MCs de remplissage sont nécessaires. Après
le dernier MC de donnée, le MC 254 indique la fin des données ou le retour
au mode ASCII. Le premier MC de remplissage est 129 et les MCs de remplissage
suivants sont calculés à l'aide de l'algorithme "253-state".
L'algorithme "253-state"
Soit P le nombre de MC depuis le début des données,
R un nombre pseudo aléatoire et MC le MC
de remplissage requis.
R = ((149 * P) MOD 253) + 1
MC = (129 + R) MOD 254
|
- Le mode ASCII. Ce mode utilise 3 manières pour encoder les caractères :
-
Caractères ASCII dans l'intervalle 0 à 127
MC = "valeur ASCII" + 1
-
Caractère ASCII étendu dans l'intervalle 128 à 255
Un premier MC de valeur 235 et un second MC avec la valeur : "valeur ASCII" - 127
-
Paire de chiffres 00, 01, 02 ..... 99
MC = "valeur numérique
de la paire de chiffres" + 130
-
Modes C40, TEXT et X12.
Les modes C40 et TEXT sont similaires nbsp;: les majuscules et les minuscules sont
seulement inversées.
Dans ces modes, 3 caractères de données sont compressés dans 2 MCs. Dans les modes
C40 et TEXT 3 caractères spéciaux (Shift) permettent de sélectionner
un autre jeu de caractères pour le caractère suivant.
la valeur sur 16 bits d'une paire de MC pair est calculée de la manière suivante :
Valeur = C1 * 1600 + C2 * 40 + C3 + 1 avec C1, C2 et C3 les valeurs des 3 caractères à compresser.
Le MC 254 indique un retour au mode ASCII sauf si ce mode permet de remplir totalement le symbole.
Dans les modes C40 et TEXT un caractère de remplissage de valeur 0 peut être ajouté
aux deux derniers caractères afin de former une paire de MC.
S'il ne reste à encoder
qu'un seul caractère en mode C40 ou TEXT ou 2 caractères en mode X12; il(s) doit(vent)
être encodé(s) en mode ASCII mais s'il ne reste qu'un seul MC de libre dans le symbole
avant les données de correction, on considère que ce MC est encodé dans le mode ASCII
sans utiliser le MC 254.
"Upper Shift" permet d'encoder un caractère ASCII étendu.
| Valeur |
Jeu de base pour C40 |
Jeu de base pour TEXT |
Jeu "Shift 1" |
Jeu "Shift 2" |
Jeu "Shift 3" pour C40 |
Jeu "Shift 3" pour TEXT |
Jeu pour X12 |
| 0 |
Shift 1 |
Shift 1 |
NUL (0) |
! (33) |
‘ (96) |
‘ (96) |
CR (13) |
| 1 |
Shift 2 |
Shift 2 |
SOH (1) |
" (34) |
a (97) |
A (65) |
* (42) |
| 2 |
Shift 3 |
Shift 3 |
STX (2) |
# (35) |
b (98) |
B (66) |
> (62) |
| 3 |
Espace (32) |
Espace (32) |
ETX (3) |
$ (36) |
c (99) |
C (67) |
Espace (32) |
| 4 |
0 (48) |
0 (48) |
EOT (4) |
% (37) |
d (100) |
D (68) |
0 (48) |
| 5 |
1 (49) |
1 (49) |
ENQ (5) |
& (38) |
e (101) |
E (69) |
1 (49) |
| 6 |
2 (50) |
2 (50) |
ACK (6) |
' (39) |
f (102) |
F (70) |
2 (50) |
| 7 |
3 (51) |
3 (51) |
BEL (7) |
( (40) |
g (103) |
G (71) |
3 (51) |
| 8 |
4 (52) |
4 (52) |
BS (8) |
) (41) |
h (104) |
H (72) |
4 (52) |
| 9 |
5 (53) |
5 (53) |
HT (9) |
* (42) |
I (105) |
I (73) |
5 (53) |
| 10 |
6 (54) |
6 (54) |
LF (10) |
+ (43) |
j (106) |
J (74) |
6 (54) |
| 11 |
7 (55) |
7 (55) |
VT (11) |
, (44) |
k (107) |
K (75) |
7 (55) |
| 12 |
8 (56) |
8 (56) |
FF (12) |
- (45) |
l (108) |
L (76) |
8 (56) |
| 13 |
9 (57) |
9 (57) |
CR (13) |
. (46) |
m (109) |
M (77) |
9 (57) |
| 14 |
A (65) |
a (97) |
SO (14) |
/ (47) |
n (110) |
N (78) |
A (65) |
| 15 |
B (66) |
b (98) |
SI (15) |
: (58) |
o (111) |
O (79) |
B (66) |
| 16 |
C (67) |
c (99) |
DLE (16) |
; (59) |
p (112) |
P (80) |
C (67) |
| 17 |
D (68) |
d (100) |
DC1 (17) |
< (60) |
q (113) |
Q (81) |
D (68) |
| 18 |
E (69) |
e (101) |
DC2 (18) |
= (61) |
r (114) |
R (82) |
E (69) |
| 19 |
F (70) |
f (102) |
DC3 (19) |
>(62) |
s (115) |
S (83) |
F (70) |
| 20 |
G (71) |
g (103) |
DC4 (20) |
? (63) |
t (116) |
T (84) |
G (71) |
| 21 |
H (72) |
h (104) |
NAK (21) |
@ (64) |
u (117) |
U (85) |
H (72) |
| 22 |
I (73) |
I (105) |
SYN (22) |
[ (91) |
v (118) |
V (86) |
I (73) |
| 23 |
J (74) |
j (106) |
ETB (23) |
\ (92) |
w (119) |
W (87) |
J (74) |
| 24 |
K (75) |
k (107) |
CAN (24) |
] (93) |
x (120) |
X (88) |
K (75) |
| 25 |
L (76) |
l (108) |
EM (25) |
^ (94) |
y (121) |
Y (89) |
L (76) |
| 26 |
M (77) |
m (109) |
SUB (26) |
_ (95) |
z (122) |
Z (90) |
M (77) |
| 27 |
N (78) |
n (110) |
ESC (27) |
FNC1 |
{ (123) |
{ (123) |
N (78) |
| 28 |
O (79) |
o (111) |
FS (28) |
|
| (124) |
| (124) |
O (79) |
| 29 |
P (80) |
p (112) |
GS (29) |
|
} (125) |
} (125) |
P (80) |
| 30 |
Q (81) |
q (113) |
RS (30) |
Upper Shift |
~ (126) |
~ (126) |
Q (81) |
| 31 |
R (82) |
r (114) |
US (31) |
|
DEL (127) |
DEL (127) |
R (82) |
| 32 |
S (83) |
s (115) |
|
|
|
|
S (83) |
| 33 |
T (84) |
t (116) |
|
|
|
|
T (84) |
| 34 |
U (85) |
u (117) |
|
|
|
|
U (85) |
| 35 |
V (86) |
v (118) |
|
|
|
|
V (86) |
| 36 |
W (87) |
w (119) |
|
|
|
|
W (87) |
| 37 |
X (88) |
x 120) |
|
|
|
|
X (88) |
| 38 |
Y (89) |
y (121) |
|
|
|
|
Y (89) |
| 39 |
Z (90) |
z (122) |
|
|
|
|
Z (90) |
|
Exemple, séquence à encoder en mode C40 : Ab
Les 3 caractères sont : 14, 02, 02
14 * 1600 +
2 * 40 + 2 + 1 = 22 483
MC1 = 22 483 \ 256 = 87
MC2 = 22 483 MOD 256 = 211
La séquence est donc : 87, 211
|
Les caractères étendus sont encodés comme suit :
- Générer le code "1" pour passer en jeu 2, puis le code 30 qui est le code "upper shift".
-
Soustraire 128 de la valeur ASCII du caractère Ã
encoder; on obtient un caractère non étendu.
- Encoder normalement ce caractère en changeant si besoin de jeu.
|
Exemple en C40:
Caractère Ë (203) : 203 - 128 = 75 soit "K", ligne
24 du jeu de base. Séquence : 1 30 24
Caractère ë (235) : 235 - 128 = 107 soit "k", ligne 11 du jeu "shift 3".
Séquence : 1 30 2 11
|
-
Mode EDIFACT.
Dans ce mode 4 caractères de données sont compressés dans 3 MCs. Chaque
caractère EDIFACT est codé sur 6 bits qui sont les 6 derniers bits de la valeur ASCII.
| Valeur EDIFACT |
>Valeur ASCII du caractère |
Commentaire |
| 0 Ã 30 |
64 Ã 94 |
Valeur EDIFACT = valeur ASCII - 64 |
| 31 |
|
Fin des données, retour au mode ASCII |
| 32 Ã 63 |
32 Ã 63 |
Valeur EDIFACT = valeur ASCII |
|
Exemple, séquence à encoder en mode EDIFACT : ABC!
Les valeurs des 4 caractères EDIFACT sont : 1, 2, 3, 33
1 * 262144 + 2 * 4096 + 3 * 64 + 33 = 270 561
MC1 = 270 561 \ 65536 = 4
MC2 = ( 270 561 MOD 65536 ) \ 256 = 32
MC3 = 270 561 MOD 256 = 225
La séquence est donc : 4, 32, 225
|
-
Mode "Base 256".
Ce mode peut encoder n'importe quel octet.
Après le MC 231 qui commute en mode "base 256" mode, il y a un champ
longueur", ce champ se compose de 1 ou 2 octets.
Soit N le nombre de données à encoder :
-
Si N < 250 un unique octet est utilisé, sa valeur
est N (de 0 Ã 249)
-
Si N >= 250 deux octets sont utilisés, la valeur du premier
est : (N \ 250) + 249 (Valeurs de 250 Ã 255) et la valeur
du second est N MOD 250 (Valeurs de 0 Ã 249).
- Si N termine le remplissage du symbole : la valeur de l'octet est 0.
De plus, chaque MC (incluant le champ de longueur) doit être calculé en utilisant l'algorithme "255-state".
|
L'algorithme "255-state".
Soit P le nombre de MC depuis le début des
données, R un nombre pseudo aléatoire,
V la valeur du MC en "base 256" et
MC le MC requis.
R = ((149 * P) MOD 255) + 1
MC = (V + R)
MOD 256
|
La détection et la correction des erreurs.
-
Le système de correction est basé sur les codes de "
Reed Solomon
" qui font la joie des matheux et la terreur des autres ...
-
Le nombre de RSs de correction dépend de la taille de la matrice. (Voir
tableau
), plus exactement il dépend de la taille des blocs.
-
Les codes de Reed Solomon font appel à un polynome dans lequel la puissance de
x est le nombre de RSs de correction d'erreur utilisé. Par exemple avec la
matrice de 8 x 8 nous utilisons une équation comme ceci : x5
+ ax4 + bx3 + cx2 + dx + e. Les nombres
a, b, c, d et e sont les facteurs de l'équation polynomiale.
-
Pour information l'équation est : (x - 2)(x - 22)(x -
23).....(x - 2k) Nous développons l'équation polynomiale
avec l'arithmetique de Galois sur chaque facteur...
Il y a 16 tailles de bloc de code de Reed Solomon (Voir tableau
) : 5, 7, 10, 11, 12, 14, 18, 20, 24, 28, 36, 42, 48, 56, 62, 68. Les facteurs
de ces 16 équations polynomiales ont étés précalculés. Vous pouvez voir le
fichier
des facteurs.
On peux aussi les calculer. Mais d'abord une petite explication sur les opérations dans un corps de Galois.
Opérations arithmétiques dans un corps de Galois de caractéristique 2.
La somme et la différence sont la même fonction : la fonction OU exclusif.
A + B = A - B = A Xor B
La multiplication est plus compliquée; d'abord nous devons créer 2 tableaux contenant
les Logs et Antilogs du corps en fonction de son "modulo" (Ici 301) :
Maintenant nous pouvons calculer Mult(a, b) = Alog((Log(a) + Log(b)) Mod 255)
|
Voici maintenant en Basic l'algorithme pour calculer les coefficients :
Et maintenant, toujours en Basic, l'algorithme de calcul des MC de correction.
Retrouvez tous les calculs des codes RS des différents codes barre 2D en Visual Basic 6.
C'est un fichier ZIP sans installation :
|
-
Ceux qui auront lus et compris les codes de Reed Solomon s'y retrouveront; pour
les quelques ignares qui n'ont pas tout compris (Dont moi !) il suffira
d'appliquer la "recette en utilisant les codes obtenus dans l'ordre inverse (Du dernier au premier).
La création des codes barres.
Maintenant que nous savons créer le motif d'un code barre, il nous reste à le dessiner
à l'écran et à l'imprimer sur papier. Deux approches sont possibles :
-
La méthode graphique où chaque barre est "dessinée" comme un rectangle plein.
Cette méthode permet de calculer la largeur de chaque barre au pixel près et de travailler
sur des multiples de la largeur d'un pixel du périphérique utilisé. Cela donne une
bonne précision surtout si le périphérique a une faible densité comme c'est le
cas des écrans et des imprimantes à jet d'encre. Cette méthode demandes des routines
de programmations spécifiques et ne permet pas de réaliser des codes barres avec un logiciel
courant.
-
La police spécifique dans laquelle chaque caractère est remplacé par le code barre
d'un caractère. Cette méthode permet d'utiliser n'importe quel programme comme un traitement
de texte ou un tableur (Par exemple LibreOffice, le clone gratuit de MSoffice !) Les mises Ã
l'échelles en fonction du corps (La taille quoi) choisi peuvent entrainer de petites distorsions du
dessin des barres. Avec une imprimante laser il n'y a aucun problème.
Il semble qu'il n'y ait pas de police gratuite pour codes barre Datamatrix
sur le net. J'ai donc décidé de dessiner entièrement cette police et de la proposer en
téléchargement. Puisque chaque symbole a un nombre pair de lignes et un nombre pair de
colonnes, je met dans chaque caractère de la police 4 modules (2 lignes et 2 colonnes). De
cette manière nous avons 16 combinaisons assignées aux 16 premières lettres majuscules.
Si nous donnons une valeur à chaque point de cette matrice de 2 X 2 comme ceci :
la valeur ASCII du caractère associé à une matrice donnée est la somme des valeurs de chaque point + 65 (65 = A = pas de point !)
La police " datamatrix.ttf "
Cette police contient les 16 caractères A (ASCII : 65) à P (ASCII : 80)
Copiez ce fichier
dans le répertoire des
polices, le plus souvent :
C:\WINDOWS\FONTS
|
Encodage d'un code datamatrix
Le programme devra se dérouler en 4 étapes :
-
Compactage des données dans les MCs en utilisant les différents modes
et en essayant d'optimiser, et si nécessaire ajout du bourrage.
-
Calcul des MCs de correction en fonction de la taille de la matrice,
et découpage en blocs si nécessaire.
- Placement des MCs dans la matrice selon l'algorithme fourni par la norme Datamatrix.
- Découpage en régions et ajout des bordures de région.
-
Transformation de chaque paire de ligne en chaine de caractère.
La longueur de la chaine est : nombre de modules / 2
Du fait de l'interaction entre les différents modes de compression il est difficile de faire
une optimisation à 100%. Le programme va donc décomposer la chaine en "blocs"
de type "numérique", "texte" ou "octet" puis il repassera certains blocs dans un autre mode
si la surcharge dûe aux MC de commutation est supérieure au gain de compression. On ne
pourra pas tenir compte de tous les paramètres tels les rembourrages ...
TRAVAIL EN COURS
Un petit programme pour tester tout ça
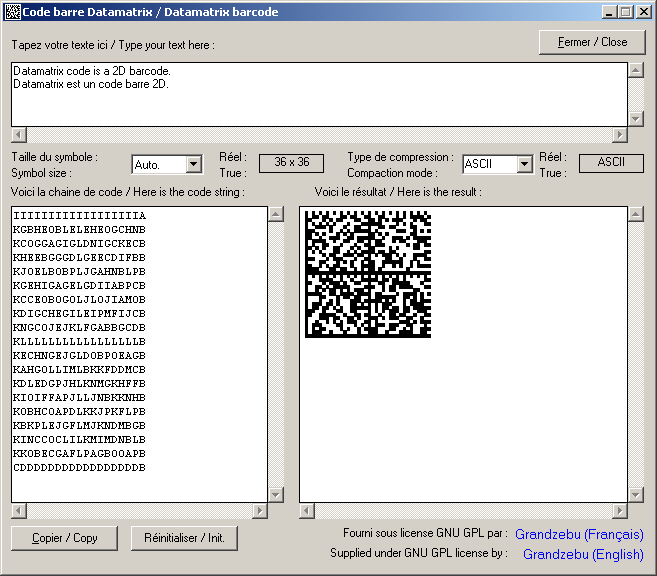
TRAVAIL EN COURS
