This code is part of the family of 2-dimensional codes, it can encode up to 2335 characters on a very
small surface. The encoding is done in two stages : first the datas are converted to 8 bits
"codeword" (High level encoding) then those are converted to small black and white squares.
(Low level encoding) Moreover an error correction system is included, it allows to reconstitute
badly printed, erased, fuzzy or torn off datas. In the continuation of this talk, the term
"codeword" will be abbreviated to CW and Reed-Solomon code in RS. There are also micro QR codes
not studied here.
The general structure.
-
The symbol is a square or rectangular array made with rows and columns. Each cell is a
small square black for a bit set to 1 and white for a bit set to 0. The dimension of the
square is named the module.
- The colors can be inverted : white on black.
-
Extended Channel Interpretation (ECI) protocol provides a method to specify particular
interpretations on byte values or to identify a particular page code.
The default ECI code is 000003 which designate the Latin alphabet ISO 8859-1.
-
There are two datamatrix standard : ECC 000-140 and ECC 200. Only
ECC 200 can be used for a new project. This study is only dedicated to the ECC 200.
- A symbol consists of one or several data regions. Each region has a one module wide perimeter.
-
Independently of the number of region, there is one, and only one, mapping
matrix. Le size of the matrix is : "region size" x "number
of region"
Example for the 36x36 symbol : "16x16" x "2x2"
---> matrix size is 32x32
Second example for the 16x48 symbol : "14x22"
x "1x2" ---> matrix size is 14x44
-
The number of rows and the number of columns (including the perimeter)
are always even (Odd for ECC 000-140 !)
- If necessary a mechanism allows to distribute more datas onse veral symbols. (Up to 16)
- The error correction mechanism is based on Reed-Solomon codes.
-
For square symbol of 48 x 48 and less, Reed-Solomon codes are appended after the datas;
for other symbols they are interleaved : datas are divided in blocks.
- Each symbol size has its own number of Reed-Solomon codes.
-
The total number of CW per symbol is equal to the number of cells
in the matrix divided by 8 (Without decimal part)
-
The 8 bits of each CW are placed in the matrix in order from left
to right and top to bottom; certain CW are split in order to fill the matrix.
- A quiet zone of 1 module (minimum) is required on the 4 sides.
-
Be careful not to confuse the concept of regions
which is a graphic division of the symbol and the concept of blocks which is a logical
division of the data.
A 2 x 2 regions code :
Low level encoding.
-
Thereafter we'll use operators : + --> addition, x --> multiplication,
\ --> integer division, MOD --> remainder of the integer division.
-
There are 24 sizes of square symbol and 6 sizes of rectangular symbol.
The following array give basic values for each symbol size.
Symbol size
Rows x columns
|
Number of
data region
(H x V)
|
Number of Reed
Solomon CW
|
Number of
block
|
|
Square symbols
|
| 10x10 |
1 |
5 |
1 |
| 12x12 |
1 |
7 |
1 |
| 14x14 |
1 |
10 |
1 |
| 16x16 |
1 |
12 |
1 |
| 18x18 |
1 |
14 |
1 |
| 20x20 |
1 |
18 |
1 |
| 22x22 |
1 |
20 |
1 |
| 24x24 |
1 |
24 |
1 |
| 26x26 |
1 |
28 |
1 |
| 32x32 |
2x2 |
36 |
1 |
| 36x36 |
2x2 |
42 |
1 |
| 40x40 |
2x2 |
48 |
1 |
| 44x44 |
2x2 |
56 |
1 |
| 48x48 |
2x2 |
68 |
1 |
| 52x52 |
2x2 |
2 x 42 |
2 |
| 64x64 |
4x4 |
2 x 56 |
2 |
| 72x72 |
4x4 |
4 x 36 |
4 |
| 80x80 |
4x4 |
4 x 48 |
4 |
| 88x88 |
4x4 |
4 x 56 |
4 |
| 96x96 |
4x4 |
4 x 68 |
4 |
| 104x104 |
4x4 |
6 x 56 |
6 |
| 120x120 |
6x6 |
6 x 68 |
6 |
| 132x132 |
6x6 |
8 x 62 |
8 |
| 144x144 |
6x6 |
10 x 62 |
8 |
|
Rectangular symbols
|
| 8x18 |
1 |
7 |
1 |
| 8x32 |
2 |
11 |
1 |
| 12x26 |
1 |
14 |
1 |
| 12x36 |
1x2 |
18 |
1 |
| 16x36 |
1x2 |
24 |
1 |
| 16x48 |
1x2 |
28 |
1 |
-
Other interesting values can be computed from these values. This is done with a spreadsheet :
-
Each region has a one module wide perimeter. Left and lower sides
are entirely black, right and top sides are made up of alternating black and white squares.
-
Each CW is placed in the matrix (If there are several regions, they are
assembled to form an unique matrix) on 45 degree parallel diagonal lines
and the left top corner is always as shown below :
In
this image, we can remark than CW nr. 2, 5 and 6 have a regular shape. CW
nr. 1, 3, 4 are truncated and the remain of these CW is reported on the
other side of the symbol. Here is the entire placement of the 8 x 8 matrix :
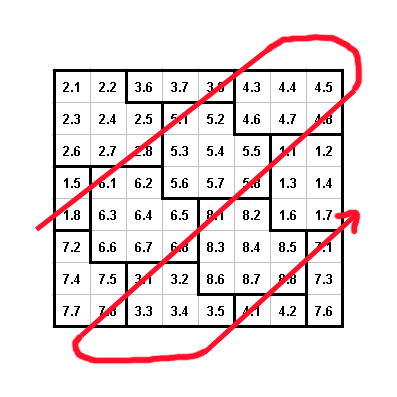You can remark on this image that the bit 8 of each CW is under the 45 degree parallel
diagonal lines. Corner and border conditions are very intricate and different for each matrix
size, fortunately Datamatrix standard give us an algorithm in order to make the placement.
High level encoding.
- The hight level encoding support six compaction mode, ASCII mode is divided in 3 sub-mode :
| Compaction mode
| Données à encoder |
Rate compaction |
| ASCII |
ASCII character 0 to 127 |
1 byte per CW |
| ASCII extended |
ASCII character 128 to 255 |
0.5 byte per CW |
| ASCII numeric |
ASCII digits |
2 byte per CW |
| C40 |
Upper-case alphanumeric |
1.5 byte per CW |
| TEXT |
Lower-case alphanumeric |
1.5 byte per CW |
| X12 |
ANSI X12 |
1.5 byte per CW |
| EDIFACT |
ASCII character 32 to 94 |
1.33 byte per CW |
| BASE 256 |
ASCII character 0 to 255 |
1 byte per CW |
-
The default character encodation method is ASCII. Some special CWs allow
to switch between the encoding methods.
| Codeword |
Data or function |
| 1 to 128 |
ASCII datas |
| 129 |
Padding |
| 130 to 229 |
Pair of digits : 00 to 999 |
| 230 |
Switch to C40 method |
| 231 |
Switch to Base 256 method |
| 232 |
FNC1 character |
| 233 |
Structure of several symbols |
| 234 |
Reader programming |
| 235 |
Shift to extended ASCII for one character |
| 236 |
Macro |
| 237 |
Macro |
| 238 |
Switch to ANSI X12 method |
| 239 |
Switch to TEXT method |
| 240 |
Switch to EDIFACT method |
| 241 |
Extended Channel Interpretation character |
| 254 |
If ASCII method is in force :
End of datas, next CWs are CW of padding
If other method is in force :
Switch back to ASCII method or indicate end of datas.
|
-
If the symbol is not full, pad CWs are required. After the last data
CW, the 254 CW indicates the end of the datas or the return to ASCII method.
First padding CW is 129 and next padding CWs are computed with the 253-state algorithm.
The 253-state algorithm.
Let P
the number of data CWs from the beginning of datas, R
a pseudo random number and CW the required
pad CW.
R = ((149 * P)
MOD 253) + 1
CW = (129 + R) MOD 254
|
- The ASCII mode. This mode has 3 ways to encode character :
-
ASCII character in the range 0 to 127
CW = "ASCII value" + 1
-
Extended ASCII character in the range 128 to 255
A first CW with
the value 235 and a second CW with the value : "ASCII value" - 127
- Pair of digits 00, 01, 02 ..... 99
CW = "Pair of digits numerical value" + 130
-
C40, TEXT and X12 modes.
C40 and TEXT modes are similar : only uppercase and lowercase characters are inverted.
In these modes 3 data characters are compacted in 2 CWs. In C40 and TEXT modes 3 shift
characters allow to indicate an other character set for the next character.
The 16 bits value of a CW pair is computed as following :
Value = C1 * 1600 + C2 * 40 + C3 + 1 with C1, C2 and C3 the 3 character values to compact.
254 CW indicate a return to the ASCII method exept if this mode allows to fill completely the symbol.
In C40 and TEXT mode a pad character with 0 value can be added at the 2 last characters
in order to form a pair of CW.
If it remains to encode only one character in
C40 or TEXT mode or 2 character in X12 mode ; it(they) must be encoded with ASCII
method but if a single free CW remain in the symbol before data correction CWs, it is
assumed that this CW is encoded using ASCII method without using the 254 CW.
"Upper Shift" character enable to encode extended ASCII character.
| Value |
Basic set for C40 |
Basic set for TEXT |
"Shift 1" set |
"Shift 2" set |
"Shift 3" set for C40 |
"Shift 3" set for TEXT |
Set for X12 |
| 0 |
Shift 1 |
Shift 1 |
NUL (0) |
! (33) |
‘ (96) |
‘ (96) |
CR (13) |
| 1 |
Shift 2 |
Shift 2 |
SOH (1) |
" (34) |
a (97) |
A (65) |
* (42) |
| 2 |
Shift 3 |
Shift 3 |
STX (2) |
# (35) |
b (98) |
B (66) |
> (62) |
| 3 |
Espace (32) |
Espace (32) |
ETX (3) |
$ (36) |
c (99) |
C (67) |
Espace (32) |
| 4 |
0 (48) |
0 (48) |
EOT (4) |
% (37) |
d (100) |
D (68) |
0 (48) |
| 5 |
1 (49) |
1 (49) |
ENQ (5) |
& (38) |
e (101) |
E (69) |
1 (49) |
| 6 |
2 (50) |
2 (50) |
ACK (6) |
' (39) |
f (102) |
F (70) |
2 (50) |
| 7 |
3 (51) |
3 (51) |
BEL (7) |
( (40) |
g (103) |
G (71) |
3 (51) |
| 8 |
4 (52) |
4 (52) |
BS (8) |
) (41) |
h (104) |
H (72) |
4 (52) |
| 9 |
5 (53) |
5 (53) |
HT (9) |
* (42) |
I (105) |
I (73) |
5 (53) |
| 10 |
6 (54) |
6 (54) |
LF (10) |
+ (43) |
j (106) |
J (74) |
6 (54) |
| 11 |
7 (55) |
7 (55) |
VT (11) |
, (44) |
k (107) |
K (75) |
7 (55) |
| 12 |
8 (56) |
8 (56) |
FF (12) |
- (45) |
l (108) |
L (76) |
8 (56) |
| 13 |
9 (57) |
9 (57) |
CR (13) |
. (46) |
m (109) |
M (77) |
9 (57) |
| 14 |
A (65) |
a (97) |
SO (14) |
/ (47) |
n (110) |
N (78) |
A (65) |
| 15 |
B (66) |
b (98) |
SI (15) |
: (58) |
o (111) |
O (79) |
B (66) |
| 16 |
C (67) |
c (99) |
DLE (16) |
; (59) |
p (112) |
P (80) |
C (67) |
| 17 |
D (68) |
d (100) |
DC1 (17) |
< (60) |
q (113) |
Q (81) |
D (68) |
| 18 |
E (69) |
e (101) |
DC2 (18) |
= (61) |
r (114) |
R (82) |
E (69) |
| 19 |
F (70) |
f (102) |
DC3 (19) |
>(62) |
s (115) |
S (83) |
F (70) |
| 20 |
G (71) |
g (103) |
DC4 (20) |
? (63) |
t (116) |
T (84) |
G (71) |
| 21 |
H (72) |
h (104) |
NAK (21) |
@ (64) |
u (117) |
U (85) |
H (72) |
| 22 |
I (73) |
I (105) |
SYN (22) |
[ (91) |
v (118) |
V (86) |
I (73) |
| 23 |
J (74) |
j (106) |
ETB (23) |
\ (92) |
w (119) |
W (87) |
J (74) |
| 24 |
K (75) |
k (107) |
CAN (24) |
] (93) |
x (120) |
X (88) |
K (75) |
| 25 |
L (76) |
l (108) |
EM (25) |
^ (94) |
y (121) |
Y (89) |
L (76) |
| 26 |
M (77) |
m (109) |
SUB (26) |
_ (95) |
z (122) |
Z (90) |
M (77) |
| 27 |
N (78) |
n (110) |
ESC (27) |
FNC1 |
{ (123) |
{ (123) |
N (78) |
| 28 |
O (79) |
o (111) |
FS (28) |
|
| (124) |
| (124) |
O (79) |
| 29 |
P (80) |
p (112) |
GS (29) |
|
} (125) |
} (125) |
P (80) |
| 30 |
Q (81) |
q (113) |
RS (30) |
Upper Shift |
~ (126) |
~ (126) |
Q (81) |
| 31 |
R (82) |
r (114) |
US (31) |
|
DEL (127) |
DEL (127) |
R (82) |
| 32 |
S (83) |
s (115) |
|
|
|
|
S (83) |
| 33 |
T (84) |
t (116) |
|
|
|
|
T (84) |
| 34 |
U (85) |
u (117) |
|
|
|
|
U (85) |
| 35 |
V (86) |
v (118) |
|
|
|
|
V (86) |
| 36 |
W (87) |
w (119) |
|
|
|
|
W (87) |
| 37 |
X (88) |
x 120) |
|
|
|
|
X (88) |
| 38 |
Y (89) |
y (121) |
|
|
|
|
Y (89) |
| 39 |
Z (90) |
z (122) |
|
|
|
|
Z (90) |
|
Sample, sequence to encode with C40 method : Ab
The 3 characters are : 14, 02, 02
14 * 1600 +
2 * 40 + 2 + 1 = 22 483
CW1
= 22 483 \ 256 = 87
CW2 = 22 483
MOD 256 = 211
The sequence is consequently : 87, 211
|
Extended characters are encoded as follows :
- Generate code "1" to switch to set 2, then the code 30 which is the "upper shift" code.
-
Substract 128 from the ASCII value of the character to encode; we obtains a
not-extended character.
- Encode normally this character with changing the set if necessary.
|
Example in C40:
Character E (203) : 203 - 128 = 75 which is "K",
line 24 of the basic set. Sequence : 1 30 24
Character e (235) : 235 - 128 = 107 which is "k",
line 11 of the "shift 3" set. Sequence : 1 30 2 11
|
-
EDIFACT mode.
In this mode 4 data characters are compacted in 3 CWs. Each EDIFACT
character is coded with 6 bits which are the 6 last bits of the ASCII value.
| EDIFACT value |
>ASCII value character |
Comment |
| 0 to 30 |
64 to 94 |
EDIFACT value = ASCII value - 64 |
| 31 |
|
End of datas, return to ASCII mode |
| 32 to 63 |
32 to 63 |
EDIFACT value = ASCII value |
|
Sample, sequence to encode with EDIFACT method : ABC!
The 4 EDIFACT character values are : 1, 2, 3, 33
1 * 262144 +
2 * 4096 + 3 * 64 + 33 = 270 561
CW1
= 270 561 \ 65536 = 4
CW2 = ( 270 561 MOD
65536 ) \ 256 = 32
CW3 = 270
561 MOD 256 = 225
The sequence is consequently : 4, 32, 225
|
-
"Base 256" mode.
This mode can encode any byte.
After the 231 CW which switch to "base 256" mode, there is a length field. This field is build with 1 or 2 bytes.
Let N the number of data to encode :
-
If N < 250 a single
byte is used, its value is N (from 0 to 249)
-
If N >= 250 two bytes are used, the value of the first one
is : (N \ 250) + 249 (Values from 250 to 255) and the
value of the second one is N MOD 250 (Values from 0 to 249).
- If N finishes the filling of the symbol : the value of the byte is 0.
Moreover each CW (including the length field) must be computed with the 255-state algorithm.
The 255-state algorithm.
Let P
the number of data CWs from the beginning of datas, R
a pseudo random number, V the base 256 CW value and
CW the required CW.
R = ((149 * P) MOD 255) + 1
CW = (V + R) MOD 256
|
Errors detection and correction.
-
The system of correction is based on the codes of "
Reed Solomon
" which make the joy of the mathematicians and the terror of the others ...
-
The number of correction CWs depend of the matrix size. (See
table
), more exactly it depend of the bloc size.
-
Reed Solomon codes are based on a polynomial equation where x power is the number of
error correction CWs used. or sample with the 8 x 8 matrix we use an equation like
this : x5 + ax4 + bx3 + cx2 + dx +
e. The numbers a, b, c, d and e are the factors of the polynomial equation.
-
For information the equation is : (x - 2)(x - 22)(x - 23).....(x
- 2k) We develop the polynomial equation with Galois arithmetic on each factor...
There is 16 Reed Solomon block size (See table
) : 5, 7, 10, 11, 12, 14, 18, 20, 24, 28, 36, 42, 48, 56, 62, 68. The factors of
these 16 polynomial equations have been pre-computed. You can see the
factors file.
We can also calculate them. But first a small explanation on the operations in a Galois body.
Arithmetic operations in a Galois body of characteristic 2.
The sum and the difference are the same function : the exclusive OR function.
A + B = A - B = A Xor B
The multiplication is more complicated ; first we need to create 2 tables containing the Logs and
Antilogs of the body according to its "modulo" (Here 301) :
Now we can calculate Mult(a, b) = Alog((Log(a) + Log(b)) Mod 255)
|
Here is now in Basic the algorithm to calculate the factors :
And now, still in Basic, the algorithm for calculating correction CWs.
Find all the RS code calculations of the different 2D barcodes in Visual Basic 6.
It is a ZIP file without installation :
|
-
Those who have read and understood the codes of Reed Solomon will find themselves there ; for the few
ignorant who have not understood everything (like me!) It will be enough to apply the "recipe" by using
the codes obtained in the reverse order (last to first).
Bar code making.
Now that we know how to create a barcode pattern, we still have to draw it on the screen and print it on
paper. Two approaches are possible :
-
The graphic method where each bar is "drawn" like a solid rectangle. This method makes it possible to
calculate the width of each bar to the nearest pixel and to work on multiples of the width of a pixel of
the used device. This gives good accuracy especially if the device has a low density as is the case of
screens and inkjet printers. This method require special programming routines and does not allow to make
bar codes with a current software.
-
The special font in which each character is replaced by a bar code. This method allow the use of any
software like a text processing or a spreadsheet. (For example LibreOffice, the free clone of MSoffice !)
The scale settings according to the selected size can bring small misshaping of the bar drawing. With
a laser printer there's no probs.
It seems there is no free fontfor datamatrix barcode on the net. I've decided
consequently to draw this font and to propose it for download. Since each symbol
have an even row number and an even column number, I put in each character of
the font 4 modules (2 rows and 2 columns). In this manner we have 16 combinations
assigned to the 16 first capital letters.
If we give a value at each dot of this 2 x 2 matrix like this :
The ASCII value of the character associated to a given matrix is the sum
each dot value + 65 (65 = A = no dot !)
The " datamatrix.ttf " font
This font contains the 16 character A (ASCII : 65) to P (ASCII : 80)
Copy this file
in the font directory,
often named :
C:\WINDOWS\FONTS
|
Encoding a datamatrix barcode
The software will evolve with 4 steps :
-
Compaction of the datas into the CWs by using of the different methods
and trying to optimize and if necessary addition of padding.
-
Calculation of the correction CWs according to the matrix size, and
splitting by blocks if necessary
-
Placement of the CWs in the matrix according to the algorithm supplied
by datamatrix standard.
- Splitting by regions and addition of the region perimeters.
-
Transformation of each row pair into a characters string.
The string length is number of module / 2
Because of the interaction between the different compaction modes it's difficult to make a
100% optimization. Thus the software will split the string into "parts" having the type
"numeric", "text" or "byte" afterwards it will change some parts for an other mode if the
overload due to switch CWs is greater than the compaction gain. We'll can't make allowance for
all the parameters like paddings, ...
WORK IN PROGRESS
A small program to test all that
WORK IN PROGRESS
