Le code PDF417

Ce code fait partie de la famille des codes à 2 dimensions, c'est en fait un code de plusieurs lignes qui peut encoder jusqu'à 2700 octets d'où son nom de "Portable Document File". L'encodage se fait en deux étapes : tout d'abord les données sont converties en "mots-clé" (Encodage de haut niveau) puis ceux-ci sont convertis en motifs de barres et d'espaces. (Encodage de bas niveau) De plus un système de correction des erreurs à plusieurs niveaux est inclus, il permet de reconstituer des données mal imprimées, effacées, floues ou arrachées. Dans la suite de cet exposé, l'expression "mot-clé" sera abrégée en MC et code de Reed-Solomon en RS.

La structure générale.

La largeur de la barre la plus fine est appelée le module.
Par la suite un module de barre est symbolisé par "1" et un module d'espace par "0".
Le code se compose de 3 à 90 lignes.
Une ligne est composée de 1 à 30 colonnes de donnés et sa largeur va de 90 à 583 modules avec les marges.
Nombre maximum de MC par code-barre : 928 dont 925 pour les données. (1 pour le descripteur de longueur et 2 au minimum pour la correction d'erreurs.)
Si nécessaire un mécanisme nommé "Macro PDF417" permet de répartir plus de données sur plusieurs codes-barre.
Il existe 929 MC dont 900 pour les données, ils sont numérotés de 0 à 928.
Le niveau de correction des erreurs va de 0 à 8. La correction comporte 2 (au niveau 0) à 512 (au niveau 8) MC.
La ligne se compose d'un caractère de début, d'un MC de coté gauche, de 1 à 30 MC de données, d'un MC de coté droit et d'un caractère de fin. Il doit y avoir une marge blanche d'au moins 2 modules de chaque coté.
Des MC de bourrage (On utilisera par exemple des "900") peuvent s'intercaler entre les MC de données et les RS de correction, ceux-ci devant être à la fin.
Le premier MC indique le nombre total de MC du code incluant : les données, les MC de bourrage et lui-même mais excluant les RS de correction.
Exemple d'un code avec 14 MC de données, un 15ème MC pour indiquer le total, un MC de bourrage et 4 RS de correction. (Niveau 1)

D é b u t	G1	D15	D14	Dr1	F i n
	G2	D13	D12	Dr2
	G3	D11	D10	Dr3
	G4	D9	D8	Dr4
	G5	D7	D6	Dr5
	G6	D5	D4	Dr6
	G7	D3	D2	Dr7
	G8	D1	D0	Dr8
	G9	C3	C2	Dr9
	G10	C1	C0	Dr10

D15 = descripteur de longueur (16 dans cet exemple)
D0 = bourrage
D1 à D14 = données
G1 à G10 = MC de coté gauche
Dr1 à Dr10 = MC de coté droit
C0 à C3 = correction d'erreur, niveau 1

L'encodage de bas biveau.

Chaque MC est codé sur 17 modules, il comprend 4 barres et 4 espaces (Le nom du code vient de là !) et il débute par une barre. Les barres et les espaces font de 1 à 6 modules de large. (Sauf pour les caractères de début et de fin) Exemple :

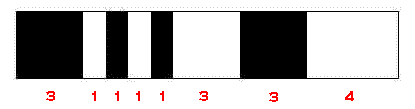
soit la formulation suivante : 111 0 1 0 1 000 111 0000
Le caractère de départ correspond à : 11111111 0 1 0 1 0 1 000
Le caractère de fin correspond à : 1111111 0 1 000 1 0 1 00 1 (Il y a ici une 5ème barre, donc 18 modules.)
Il existe 3 tables distinctes pour encoder les 929 MC.
Les 3 tables donnant les motifs des 929 MC commencent comme ceci :

Première table	Deuxième table	Troisième table	Fichier complet des tables :
111 0 1 0 1 0 111 000000	11111 0 1 0 1 0 11 00000	11 0 1 0 1 0 11111 00000
1111 0 1 0 1 0 1111 0000	111111 0 1 0 1 0 111 000	111 0 1 0 1 0 111111 000
11111 0 1 0 1 0 11111 00	1111 0 1 0 1 00 1 000000	1 0 1 0 1 00 1111 000000
111 0 1 0 1 00 111 00000	11111 0 1 0 1 00 11 0000	11 0 1 0 1 00 11111 0000
.....	.....	.....

Chaque ligne n'utilise qu'une table de codage qui sera réutilisée ensuite 3 lignes plus loin. Exemple : Ligne 1 --> table 1, ligne 2 --> table 2, ligne 3 --> table 3, ligne 4 --> table 1, .....etc. On a la formule : N° table = ( ( N° ligne MOD 3 ) * 3 )

L'encodage de haut biveau.

On utilisera par la suite les opérateurs : + --> addition, x --> multiplication, \ --> division entière, MOD --> reste de la division entière.
Les données sont compressées dans les MC selon 3 modes conçus en fonction de leur efficacité par rapport au type des données. Le mode par défaut est le mode "Texte".

Type de compression	Données à coder	Taux de compression
"Octet"	ASCII 0 à 255	1,2 octet par MC
"Texte"	ASCII 9, 10, 13 & 32 à 127	2 caractères par MC
"Numérique"	Chiffres seuls 0 à 9	2,9 chiffres par MC

Les MC numérotés 900 à 928 ont une signification spéciale, certains permettent de passer d'un mode à l'autre afin d'optimiser le code.

MC numéro :	Fonction
900	Passer en mode "Texte"
901	Passer en mode "Octet"
902	Passer en mode "Numérique"
903 à 912	Réservé
913	Passer en mode "Octet" pour le prochain MC
914 à 920	Réservé
921	Initialisation
922	Terminaison de bloc pour les macro PDF
923	Séquence d'identification de champ dans un macro PDF
924	Passer en mode "Octet" (Si nombre d'octet multiple de 6)
925	Identifiant personnalisé ECI
926	Identifiant général ECI
927	Identifiant ECI pour jeu de caractères ou page de code
928	Début de bloc pour les macro PDF

Le mode "Texte" possède 4 sous-modes :

Majuscules
Minuscules
Mixte : Numérique et ponctuation
Ponctuation

Le sous-mode par défaut est "Majuscules", dans ce sous-mode deux caractères sont codés dans chaque MC, voici la table des caractères :

Valeur	Majuscules	Minuscules	Mixte	Ponctuation
0	A	a	0	;
1	B	b	1	<
2	C	c	2	>
3	D	d	3	@
4	E	e	4	[
5	F	f	5	\
6	G	g	6	]
7	H	h	7	_
8	I	i	8	` (Quote)
9	J	j	9	~
10	K	k	&	!
11	L	l	CR	CR
12	M	m	HT	HT
13	N	n	,	,
14	O	o	:	:
15	P	p	#	LF
16	Q	q	-	-
17	R	r	.	.
18	S	s	$	$
19	T	t	/	/
20	U	u	+	“
21	V	v	%	\|
22	W	w	*	*
23	X	x	=	(
24	Y	y	^	)
25	Z	z	PON	?
26	SP	SP	SP	{
27	MIN	T_MAJ	MIN	}
28	MIX	MIX	MAJ	' (Apostrophe)
29	T_PON	T_PON	T_PON	MAJ

Cette table contient 6 commutateurs permettant de changer de sous-mode :
MAJ : passer en "Majuscules"
MIN : passer en "Minuscules"
MIX : Passer en "Mixte"
PON : passer en "Ponctuation"
T_MAJ : passer en "Majuscules" pour le caractère suivant
T_PON : passer en "Ponctuation" pour le caractère suivant
Les caractères sont codés par paire; soit C₁ et C₂ les valeurs de deux caractères, la valeur du MC est : C₁ x 30 + C₂
S'il reste un caractère seul, on lui ajoute un commutateur en guise de bourrage, par exemple T_PON.

Exemple, séquence à encoder : Super !

S : 18, MIN : 27, u : 20, p : 15, e : 4, r : 17, ESPACE : 26, T_PON : 29, ! : 10
soit 9 caractères, on rajoutera un T_PON de bourrage.
MC₁ = 18 x 30 + 27 = 567
MC₂ = 20 x 30 + 15 = 615
MC₃ = 4 x 30 + 17 = 137
MC₄ = 26 * 30 + 29 = 809
MC₅ = 10 x 30 + 29 = 329
La séquence est donc : 567, 615, 137, 809, 329

Le mode "Octet" permet de coder 256 octets différents, c'est à dire la table ASCII étendue entière.
Si le nombre d'octet est un multiple de 6, on utilise le commutateur 924 pour passer en mode "Octet", si le nombre d'octet n'est pas un multiple de 6 on utilise le MC 901 pour la commutation.
Le codage consiste à transformer 6 octets en base 256 en 5 MC en base 900. Pour effectuer la conversion :

Prendre les octets par groupe de 6; soit X₅ à X₀ leurs valeurs décimales. (X₀ est le caractère de poids le plus faible)
Calculer la somme S = X₅ x 256⁵ + X₄ x 256⁴ + X₃ x 256³ + X₂ x 256² + X₁ x 256 + X₀
Calculons les MC : MC₀ = S MOD 900, nouvelle valeur de S : S = S \ 900, MC₁ = S MOD 900 ... etc jusqu'à MC4 (MC₀ est le MC de poids le plus faible)
S'il reste des octets après avoir transformé les groupes de 6, les prendre tels quel : 1 octet = 1 MC de même valeur.

Exemple 1 : séquence à encoder : alcool

La suite d'octets (En ASCII) est donc : 97, 108, 99, 111, 111, 108
S = 97 x 256⁵ + 108 x 256⁴ + 99 x 256³ + 111 x 256² + 111 x 256 + 108 = 107 118 152 609 644
MC₀ = 107 118 152 609 644 MOD 900 = 244
S = 107 118 152 609 644 \ 900 = 119 020 169 566
MC₁ = 119 020 169 566 MOD 900 = 766
S = 119 020 169 566 \ 900 = 132 244 632
MC₂ = 132 244 632 MOD 900 = 432
S = 132 244 632 \ 900 = 146 938
MC3 = 146 938 MOD 900 = 238
S = 146 938 \ 900 = 163
MC4 = 163 MOD 900 = 163
La séquence incluant le commutateur est donc : 924, 163, 238, 432, 766, 244

Exemple 2 : séquence à encoder : alcoolique

La suite d'octets (En ASCII) est donc : 97, 108, 99, 111, 111, 108, 105, 113, 117, 101
Les 6 premiers octets se codent comme ci-dessus et on ajoute 105, 113, 117 et 101
La séquence incluant le commutateur est donc : 901, 163, 238, 432, 766, 244, 105, 113, 117, 101

Le mode "Numérique" est une conversion de base 10 en base 900
Pour effectuer la conversion :

Prendre les chiffres par groupe de 44 (ou moins pour ce qui reste)
Ajouter le chiffre 1 en tête, celui-ci sera retiré par la procédure de décodage
Effectuer un changement de base comme pour le mode "Octet"
Les groupes de 44 chiffres donnent 15 MC
Les groupes plus petits donnent un nombre de MC égal à : Nombre de chiffres \ 3 + 1
Exemple : 10 chiffres donnent 10 \ 3 + 1 = 3 + 1 = 4 MC

Exemple, séquence à encoder : 01234

Il y aura donc 5 \ 3 + 1 = 2 MC
Ajouter un 1 devant : 101234
MC₀ = 101 234 MOD 900 = 434
S = 101 234 \ 900 = 112
MC₁ = 112 MOD 900 = 112
La séquence est donc : 112, 434

Les MC de coté gauche et de coté droit se calculent en fonction de la table utilisée pour la ligne considérée.
Pour obtenir la valeur du MC, faire le calcul suivant : (N° ligne \ 3) x 30 + X avec X à prendre dans la table suivante. (La première ligne porte le numéro 0)

N° de table utilisée pour encoder les MC de cette ligne	X pour le MC de coté gauche	X pour le MC de coté droit
1	(Nombre de lignes -1) \ 3	Nombre de colonnes de données - 1
2	(Niveau de sécurité x 3) + (Nombre de lignes -1) MOD 3	(Nombre de lignes -1) \ 3
3	Nombre de colonnes de données - 1	(Niveau de sécurité x 3) + (Nombre de lignes -1) MOD 3

La détection et la correction des erreurs.

Le système de détection d'erreur utilise 2 MC et le système de correction en utilise de 2 à 510
Le système de correction utilise les codes de " Reed Solomon " qui font la joie des matheux et la terreur des autres...
Le nombre de RS à ajouter au code est fonction du niveau de correction que l'on applique, du fait de la limitation du code à 928 MC (Dont 1 pour le nombre de MC) le niveau maximum est limité par le nombre de MC de données. Le nombre de MC que l'algorithme de correction des erreurs peut reconstituer est égal au nombre de RS requis par le système de correction : ce n'est pas de la magie mais des maths !

Niveau	Nombre de RS requis par la correction dont 2 pour la détection ( 2^{niveau + 1})	Nombre maximum de MC de données
0	2	925
1	4	923
2	8	919
3	16	911
4	32	895
5	64	863
6	128	799
7	256	671
8	512	415

Le niveau de correction des erreurs recommandé est fonction du nombre de MC de données :

Nombre de MC de données	Niveau recommandé
1 à 40	2
41 à 160	3
161 à 320	4
321 à 863	5

Les codes de Reed Solomon font appel à un polynome d'ordre égal à 2^s+1 avec s = niveau de correction choisi. Par exemple avec le niveau 1 on utilise un polynome de la forme a + bx + cx² + dx³ + x⁴ Les nombres a, b, c et d sont les coefficients du polynome.
Pour information le polynome est : (x - 3)(x - 3²)(x - 3³).....(x - 3^k) ( avec k = 2^s+1 ) On développe le polynome et on fait un MOD 929 sur chaque coefficient. Ces coefficients ont étés précalculés pour les 8 polynomes correspondant aux 8 niveaux de correction. Vous pouvez consulter le fichier des coefficients. On peux aussi les calculer.

Voici en Basic l'algorithme pour calculer les coefficients :

Soit s le niveau de correction utilisé, k = 2^s+1 le nombre de RS.
Voyons maintenant, toujours en Basic, l'algorithme de calcul des codes de RS.

Retrouvez tous les calculs des codes RS des différents codes barre 2D en Visual Basic 6.
C'est un fichier ZIP sans installation :

Ceux qui auront lus et compris les codes de Reed Solomon s'y retrouveront ; pour les quelques ignares qui n'ont pas tout compris (Dont moi !) il suffira d'appliquer la "recette" en utilisant les codes obtenus dans l'ordre inverse (Du dernier au premier).

La création des codes barres.

Maintenant que nous savons créer le motif d'un code barre, il nous reste à le dessiner à l'écran et à l'imprimer sur papier. Deux approches sont possibles :

La méthode graphique où chaque barre est "dessinée" comme un rectangle plein. Cette méthode permet de calculer la largeur de chaque barre au pixel près et de travailler sur des multiples de la largeur d'un pixel du périphérique utilisé. Cela donne une bonne précision surtout si le périphérique a une faible densité comme c'est le cas des écrans et des imprimantes à jet d'encre. Cette méthode demandes des routines de programmations spécifiques et ne permet pas de réaliser des codes barres avec un logiciel courant.
La police spécifique dans laquelle chaque caractère est remplacé par le code barre d'un caractère. Cette méthode permet d'utiliser n'importe quel programme comme un traitement de texte ou un tableur (Par exemple LibreOffice, le clone gratuit de MSoffice !) Les mises à l'échelles en fonction du corps (La taille quoi) choisi peuvent entrainer de petites distorsions du dessin des barres. Avec une imprimante laser il n'y a aucun problème.

Il semble qu'il n'y ait pas de police gratuite pour codes barre PDF417 sur le net. J'ai donc décidé de dessiner entièrement cette police et de la proposer en téléchargement. Le fait qu'il y ait 929 MC avec pour chacun 3 variantes va nous obliger à diviser les 17 bits d'un MC en plusieurs parties. Mais diviser 17 ... hein ... il va falloir ruser. Si l'on considère que le premier bit est toujours "1" et le dernier "0", on peut imaginer un séparateur de forme "01" et il ne reste plus que 15 bits dans chaque MC; on peut alors diviser ces 15 bits en 3 quintets,. Il existera alors 2⁵ = 32 quintets possibles affectés à 32 caractères de la police. Le programme d'encodage sera chargé de transformer les 3 quintets de chaque MC en une chaine de 3 caractères.
La police va donc contenir les caractères suivants :

Caractères A (ASCII : 65) à F (ASCII :70) et a (ASCII : 97) à z (ASCII :122) pour les 32 quintets de formule "00000" à "11111"
Caractère * (ASCII : 42) pour le séparateur de formule "01"
Caractère + (ASCII : 43) pour le caractère de début de ligne amputé de son 0 final, formule "11111111 0 1 0 1 0 1 00"
Caractère - (ASCII : 45) pour le caractère de fin de ligne amputé de son premier 1, formule "111111 0 1 000 1 0 1 00 1"

La chaine de caractère à envoyer à l'imprimante ressemblera donc à quelque chose comme : +*gfA*jhD*BAl*gCt*hjk*- et ceci pour chaque ligne.

La police " pdf417.ttf "

Cette police contient les 35 motifs décrits ci-dessus. Les codes de début de ligne et de fin de ligne intégrent des marges de 2 modules. La hauteur est égale à 3 modules ce qui correspond au cas le plus courant.

Copiez ce fichier
dans le répertoire des
polices, le plus souvent :
C:\WINDOWS\FONTS

Encodage d'un code pdf417

Le programme devra se dérouler en 4 étapes :

Compactage des données dans les MC en utilisant les différents modes et en essayant d'optimiser.
Calcul des MC de correction en fonction du niveau de sécurité choisi.
Découpage en lignes et ajout des MC de coté gauche et droit
Transformation de chaque MC en chaine de 3 caractères et ajout des séparateurs, des débuts de ligne, des fins de ligne et des retours chariot.

Du fait de l'interaction entre les différents modes de compression et les différents sous-modes du mode "texte" il est difficile de faire une optimisation à 100%. Le programme va donc décomposer la chaine en "blocs" de type "numérique", "texte" ou "octet" puis il repassera certains blocs dans un autre mode si la surcharge dûe aux MC de commutation est supérieure au gain de compression. On ne pourra pas tenir compte de tous les paramètres tels les rembourrages, les gains sur les multiples de 6 octets, les commutateurs mono-caractère ou les commutations entres sous-modes du mode "texte" : il faudrait pour cela plusieurs milliers de lignes de programme.
Une autre difficulté vient de la grandeur des nombres manipulés, par exemple l'opération "Modulo 900" appliquée à un nombre de 44 chiffres engendre inévitablement un dépassement de capacité; le programme devra effectuer ce type de calcul par étapes.

Un petit programme pour tester tout ça

Voici un petit programme écrit
en Visual Basic 6. Le fichier
d'installation copiera le
programme, les dépendances
Visual Basic ainsi que les
fichiers sources et la police.

Fichier d'auto-installation :

Fichier ZIP sans installation :

La fonction PDF417$ fait environ 500 lignes, je ne la reproduis donc pas ici, il suffit de la récuperer dans le fichier "form1.frm" qui se trouve avec le programme ci-dessus ; avec le programme d'auto-installation le fichier "form1.frm" se trouve dans le répertoire du programme, sous-répertoire "sources".
La fonction s'appelle de la manière suivante : resultat$ = pdf417$(Chaine$, Sécu%, NbCol%, CodeErr%)
avec Chaine$ qui doit contenir la chaine à coder, Sécu% pour le niveau de correction (-1 = auto.), NbCol% pour le nombre de colonnes de données par ligne (<1 = auto.) et CodeErr% pour récupérer un éventuel numéro d'erreur. Ces trois derniers paramètres sont optionnels et sont passés par références; au retour ils contiennent les valeurs réellement utilisées. Valeurs de CodeErr% au retour de la fonction :

1 : Chaine$ est vide
2 : Chaine$ contient trop de données, on dépasse le nombre de 928 MC.
3 : Nombre de MC par ligne trop faible, on dépasse 90 lignes.
10 : Le niveau de sécurité a été abaissé pour ne pas dépasser les 928 MC. (Ce n'est pas une erreur mais une alerte.)

Il suffit maintenant d'afficher ou d'imprimer la chaine resultat$ avec la police pdf417 par exemple dans un traitement de texte. Les utilisateurs de Word pourront même intégrer la fonction pdf417$ dans une macro afin d'automatiser le traitement. Pour arriver à effectuer tous les traitements dans une unique fonction, j'ai dû utiliser des "Gosub" au lieu de fonctions avec paramètres; j'entends déjà les esthètes de la programmation hurler au sacrilège.

Vous aimez cette page ?

Elle vous est utile ?

Index des mots-clés