Le QRcode

Ce code fait partie de la famille des codes à 2 dimensions, il peut encoder jusqu'à 7089 caractères sur une très petite surface. L'encodage se fait en deux étapes : tout d'abord les données sont converties en un flux de bit découpé en mots-clé. (Encodage de haut niveau) puis ceux-ci sont convertis en petits carrés noirs et blancs. (Encodage de bas niveau) De plus un système de correction des erreurs permet de reconstituer des données mal imprimées, effacées, floues ou arrachées. Dans la suite de cet exposé, l'expression "mot-clé" sera abrégée en MC et code de Reed-Solomon en RS. Il existe aussi des micro QR codes non étudiés ici.

La structure générale.

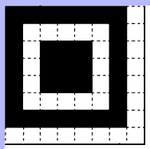
Le symbole est une zone carrée constituée de lignes et colonnes (Numérotées à partir de 0). Chaque cellule est un petit carré noir ou blanc appelé module. Le symbole comporte 3 motifs de repérage aux coins supérieurs et inférieur gauche le rendant bien reconnaissable. La dimension du symbole est appelée la version, il en existe 40 ayant de 21 à 177 modules (par pas de 4 modules). Le niveau de correction (parmi 4) est noté L, M, Q ou H
Les couleurs peuvent être interverties : blanc sur noir ; le symbole peux aussi être retourné par effet miroir.
Le protocole ECI (Extended Channel Interpretation) procure un mode pour spécifier une interprétation particulière des valeurs des octets ou pour identifier une page de code particulière.
Par défaut le code ECI est 000003 qui désigne l'alphabet Latin ISO 8859-1.
Si nécessaire un mécanisme permet de répartir plus de données sur plusieurs symboles. (Jusqu'à 16)
Le mécanisme de correction des erreurs est basé sur les codes de Reed-Solomon.
Le symbole comporte un certains nombre de modules de fonction :
- Les 3 motifs de repérage de 8 x 8 modules
- Des mires d'alignement de 5 x 5 modules (position : voir tableau)
- 2 bandes de synchronisation alternant module blanc et noir, une horizontale en ligne 6 et une verticale en colonne 6
- Des zones d'information de format et de version accolées aux motifs de repérage
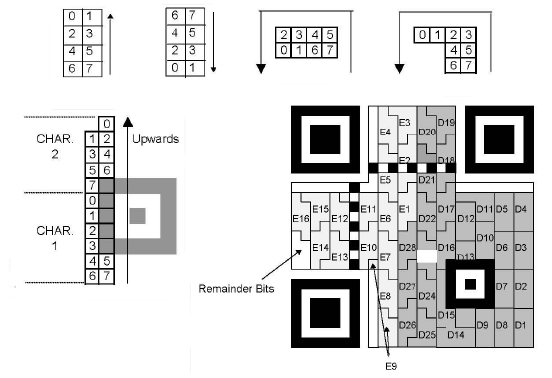
Les modules de fonctions (mires, synchro, info,...) étant placés, les données sont placées en partant du coin inférieur droit en allant de droite à gauche, d'abord en montant puis en redescendant et en contournant tous les modules de fonction.
Une marge blanche de 4 modules doit encadrer le code.

L'encodage de bas niveau.

Il existe 40 versions (Tailles) de symbole. Un ensemble de paramètres est attaché à chaque version :

Le numéro de version.
Le premier espacement des mires d'alignement
Le deuxième espacement des mires d'alignement
Le nombre de bits pour les 4 indicateurs de taille en mode numérique, alphanumérique, octet et Kanji (Voir encodage de haut niveau)
Pour chacun des 4 niveaux de correction d'erreurs (Voir encodage de haut niveau)
- Le nombre de blocs dans lesquels répartir les données
- Le nombre de RS par bloc

A partir de ces paramètres nous pouvons calculer d'autres valeurs, cela est fait à l'aide d'une feuille de calcul :

On va y trouver le calcul de la taille du symbole, du nombre et de l'emplacement des mires d'alignement, les surfaces occupées par les différents éléments, etc ...

Pour construire un QRcode il faut :

Placer les 3 repères aux coins supérieurs et inférieur gauche.
Les repères ont une taille de 8 x 8 en comptant une marge de 1 module sur les 2 cotés internes ; ci-dessous le coin supérieur gauche :

Tracer les lignes de synchronisation en ligne et colonne 6
Placer les mires d'alignement. Celles-ci ont une taille de 5 X 5.
Leur centre est placé à l'intersection d'un quadrillage dont les numéros de ligne sont identiques aux numéros de colonne, on va par la suite appeler ces numéros L/C.
Le premier L/C est toujours 6. Les 3 mires qui viendraient en collision avec les repères d'angle sont supprimées.
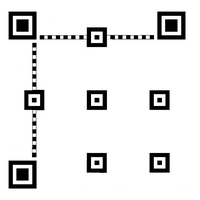
Par exemple dans le dessin ci-dessous on a 3 L/C, le nombre de mires est (3 x 3) -3 = 6. Avec 4 L/C on aurait (4 x 4) - 3 = 13 mires.
Il y a dans la feuille de calcul 2 colonnes d'espacement à utiliser comme suit :
- 2ème L/C = 6 (qui est le 1er L/C) + espacement 1
- 3ème L/C (et suivants) = L/C précédent + espacement 2

Réserver les emplacements destinés aux informations de format.
L'information de format est une séquence de 15 bits : 5 de données et 10 de codes de correction d'erreur de type BCH
Les 5 bits de données sont :
   2 bits indiquant le niveau de correction du code : L (01), M (00), Q (11) ou H (10)
   3 bits indiquant le motif de masque utilisé (Voir plus bas le masquage)
Les 10 bits de correction sont calculés de la manière suivante :
   Les 5 bits de données sont les coefficients d'un polynôme d'ordre 14 ; exemple 01001 donne X¹³ + X¹⁰
   On divise ce polynôme par X¹⁰ + X⁸ + X⁵ + X⁴ + X² + X + 1 (Les coefficients de ce polynôme sont : 10100110111)
   Les coefficients du reste de la division sont les 10 bits de correction à ajouter aux 5 bits de donnée.
Finalement on applique le masque 101010000010010 en faisant un XOR avec les 15 bits obtenus précédemment.

Les informations de format sont placées à 2 endroits occupant au total 31 modules (dont 1 toujours noir)

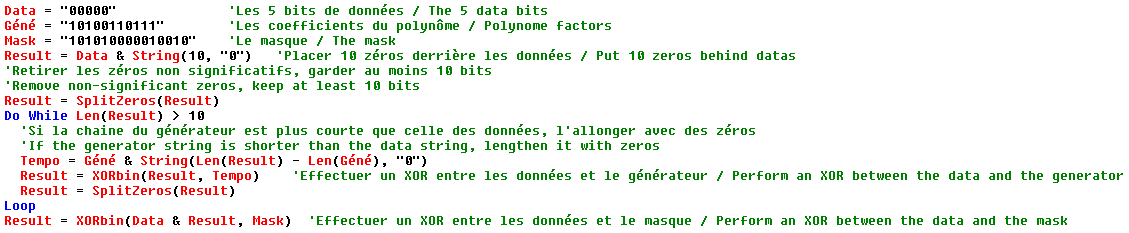
L'algorithme de création de la chaîne de format en Basic :
Pour les codes de version 7 et plus, il faut ajouter des informations de version.
L'information de version est une séquence de 18 bits : 6 bits de données et 12 de codes de correction d'erreur de type Golay.
Les 6 bits de données représentent le numéro de version.
Les 12 bits de correction sont calculés de la manière suivante :
   Les 6 bits de données sont les coefficients d'un polynôme d'ordre 17 ; exemple pour la version 9 : 001001 donne X¹⁵ + X¹²
   On divise ce polynôme par X¹² + X¹¹ + X¹⁰ + X⁹ + X⁸ + X⁵ + X² + 1
   Les coefficients du reste de la division sont les 12 bits de correction à ajouter aux 6 bits de donnée.

Les informations de version sont placées à 2 endroits occupant au total 36 modules

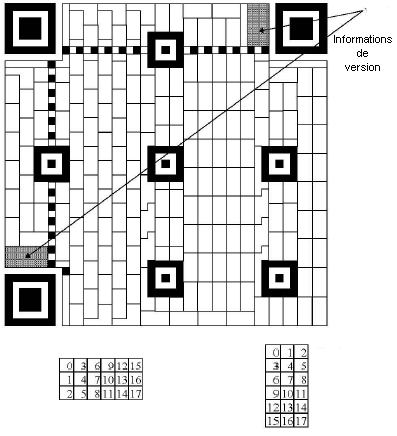
L'algorithme de création de la chaîne de version en Basic :

Maintenant passons au placement des modules de données et de correction, on commence dans le coin inférieur droit et en montant sur 2 colonnes de modules. Les bits de chaque MC sont placés en commençant par le dernier. On place les bits d'abord dans la colonne de droite puis dans celle de gauche et on contourne les modules de fonction. Arrivé en haut on redescend sur les 2 colonnes adjacentes à gauche toujours dans l'ordre droite-gauche.

Afin d'obtenir un code barre aussi équilibré que possible il faut maintenant appliquer à la zone des données et codes de correction un masque. Le masquage consiste à appliquer une opération XOR entre la donnée de chaque module et le module correspondant du masque.
Il existe 8 masques différents et il va falloir trouver celui qui donne le résultat le plus équilibré :
- Rapport blanc sur noir proche de 1
- Si possible, pas de motif 1011101
- Aussi peu de "gros" blocs que possible.
Le numéro du masque choisi sera indiqué dans les informations de format. Dans le tableau suivant se trouvent les 8 types de masque avec la fonction permettant de définir le motif du masque. Tout module pour lequel la condition est vraie sera noir. Dans la formule de condition i et j sont respectivement le numéro de ligne et de colonne du module. i = j = 0 correspond au coin supérieur gauche.

Numéro de masque Condition

000 (i + j) MOD 2 = 0
001 i MOD 2 = 0

010 j MOD 3 = 0

011 (i + j) MOD 3 = 0

100 ((i DIV 2) + (j DIV 3)) MOD 2 = 0

101 (i j) MOD 2 + (i j) MOD 3 = 0

110 ((i j) MOD 2 + (i j) MOD 3) MOD 2 = 0

111 ((i + j) MOD 2 + (i j) MOD 3) MOD 2 = 0

L'encodage de haut niveau
On utilisera par la suite les opérateurs : + --> addition, x --> multiplication, \ --> division entière, MOD --> reste de la division entière
Il existe 4 modes d'encodage (Compression) qui peuvent être mixés :

Mode de compression Données à encoder Taux de compression Indicateur de mode

Numérique Chiffres ASCII 3 chiffres dans 10 bits 0001

Alphanumérique Chiffres + lettres majuscules + 9 symboles 2 caractéres dans 11 bits 0010

Octet Octet 1 octet dans 8 bits 0100

Kanji Caractères asiatiques / 1000

Il existe d'autres indicateurs non étudiés ici : 0111 = ECI, 0011 = Multi codes, 0101 et 1001 = FNC1
0000 est l'indicateur de fin de données.

Chaque segment commence par un indicateur de mode de 4 bits suivi du nombre de caractères codé sur un nombre de bit variable (Voir tableau), suivi des données.

Les segments de chaque mode sont ensuite concaténés puis suivis d'un terminateur composé de 4 zéros qui est l'indicateur de fin des données.

Le terminateur peut être abrégé si cela permet le remplissage complet de la zone des données d'un symbole.

Ce flux est alors découpés en MC de 8 bits. Si nécessaire, le dernier MC est ajusté à 8 bits par ajout de bits 0. Si le nombre de MC ne remplit pas complètement le symbole ajouter 11101100 puis 00010001 et recommencer (236 et 17 en décimal)

Les MCs sont alors divisés en un certain nombre de blocs (Voir tableau) La taille des blocs peux varier de une unité; par exemple 46 MCs divisés en 4 blocs donneront 2 blocs de 11 et 2 blocs de 12. Dans ce cas, on placera les plus petits blocs en premier.

Pour chaque bloc les codes de Reed Solomon sont calculés.

Pour finir on entrelacera les données puis les codes de RS comme suit :
n est le nombre de blocs, m le nombre de MC dans chaque bloc et z le nombre de codes de RS par bloc
data 1 du bloc 1 - data 1 du bloc 2 - ... - data 1 du bloc n
data 2 du bloc 1 - data 2 du bloc 2 - ... - data 2 du bloc n
...
data m du bloc 1 - data m du bloc 2 - ... - data m du bloc n
puis :
RS 1 du bloc 1 - RS 1 du bloc 2 - ... - RS 1 du bloc n
RS 2 du bloc 1 - RS 2 du bloc 2 - ... - RS 2 du bloc n
...
RS z du bloc 1 - RS m du bloc 2 - ... - RS z du bloc n

Le mode numérique.
Dans ce mode on divise les données en groupes de 3 chiffres qui sont compressés dans 10 bits.
S'il ne reste que 2 chiffres on les converti sur 7 bits et s'il ne reste qu'un chiffre on le converti sur 4 bits. Le segment comprendra donc : l'indicateur de mode 0001, le compteur de caractères (Longueur à prendre dans le tableau) et les données.

Exemple :
Chaine : 34567
Premier groupe : 345 soit 0101011001
2ème groupe : 67 soit 1000011
Nombre de caractères : 5
Si code de version 3 par exemple, longueur sur 9 bits, soit : 000000101
Segment : 0001 000000101 0101011001 1000011

Le mode alphanumérique.
Dans ce mode on ne peux encoder que 45 caractères numérotés 0 à 44 selon le tableau suivant :

Valeur Caractère Valeur Caractère Valeur Caractère Valeur Caractère

0 0 13 D 26 Q 39 *

1 1 14 E 27 R 40 +

2 2 15 F 28 S 41 -

3 3 16 G 29 T 42 .

4 4 17 H 30 U 43 /

5 5 18 I 31 V 44 :

6 6 19 J 32 W

7 7 20 K 33 X

8 8 21 L 34 Y

9 9 22 M 35 Z

10 A 23 N 36 (Espace)

11 B 24 O 37 $

12 C 25 P 38 %

Les caractères sont pris deux par deux et encodés sur 11 bits. Le code du premier caractère est multiplié par 45, on ajoute alors le code du 2ème caractère et la somme est convertie en binaire sur 11 bits.
S'il reste un unique caractère, son code est converti en binaire sur 6 bits.

Exemple :
Chaine : ZEBU Séquence : 35 14 11 30
Premier groupe : 35 x 45 + 14 = 1589 soit 11000110101
2ème groupe : 11 x 45 + 30 = 525 soit 01000001101
Nombre de caractères : 4
Si code de version 3 par exemple, longueur sur 10 bits, soit : 0000000100
Segment : 0010 0000000100 11000110101 01000001101

Le mode octet.
Ce mode peut encoder n'importe quel octet.
Ceux-ci sont simplement convertis en binaire.

Le mode Kanji.
Ce mode n'est pas étudié ici.

La détection et la correction des erreurs.

Le système de correction est basé sur les codes de " Reed Solomon "qui font la joie des matheux et la terreur des autres ...

Le nombre de MCs de correction dépend de la version du code et du niveau de correction choisi ; il est donné pour chaque bloc de données. (Voir tableau)

Les codes de Reed Solomon font appel à un polynome dans lequel la puissance de x est le nombre de MCs de correction d'erreur utilisé. Par exemple pour un code version 1 avec niveau de correction L nous utilisons une équation permettant d'obtenir 7 RS comme ceci : x⁷ + ax⁶ + bx⁵ + cx⁴ + dx³ + ex² + fx + g Les nombres a, b, c, d, e, f et g sont les coefficients de l'équation polynomiale.

Pour information l'équation est : x⁸ + x⁴ + x³ + x² + 1 et le corps de Galois se calcule avec modulo 285.
Il y a 36 tailles de bloc de code de Reed Solomon (Voir tableau) en incluant les micro-qrcodes. Les coefficients de ces 36 équations polynomiales ont étés précalculés. Vous pouvez voir le fichier des coefficients. On peux aussi les calculer. Mais d'abord une petite explication sur les opérations dans un corps de Galois.

Opérations arithmétiques dans un corps de Galois de caractéristique 2.

La somme et la différence sont la même fonction : la fonction OU exclusif.
A + B = A - B = A Xor B
La multiplication est plus compliquée; d'abord nous devons créer 2 tableaux contenant les Logs et Antilogs du corps en fonction de son "modulo" (Ici 285) :

Maintenant nous pouvons calculer Mult(a, b) = Alog((Log(a) + Log(b)) Mod 255)

Voici maintenant en Basic l'algorithme pour calculer les facteurs :

Et maintenant, toujours en Basic, l'algorithme de calcul des MC de correction.

Retrouvez tous les calculs des codes RS des différents codes barre 2D en Visual Basic 6.
C'est un fichier ZIP sans installation :

Ceux qui auront lus et compris les codes de Reed Solomon s'y retrouveront; pour les quelques ignares qui n'ont pas tout compris (Dont moi !) il suffira d'appliquer la "recette" en utilisant les codes obtenus dans l'ordre inverse (Du dernier au premier).

La création des codes barres.
Maintenant que nous savons créer le motif d'un code barre, il nous reste à le dessiner à l'écran et à l'imprimer sur papier. Deux approches sont possibles :

La méthode graphique où chaque barre est "dessinée" comme un rectangle plein. Cette méthode permet de calculer la largeur de chaque barre au pixel près et de travailler sur des multiples de la largeur d'un pixel du périphérique utilisé. Cela donne une bonne précision surtout si le périphérique a une faible densité comme c'est le cas des écrans et des imprimantes à jet d'encre. Cette méthode demandes des routines de programmations spécifiques et ne permet pas de réaliser des codes barres avec un logiciel courant.

La police spécifique dans laquelle chaque caractère est remplacé par le code barre d'un caractère. Cette méthode permet d'utiliser n'importe quel programme comme un traitement de texte ou un tableur (Par exemple LibreOffice, le clone gratuit de MSoffice !) Les mises à l'échelles en fonction du corps (La taille quoi) choisi peuvent entrainer de petites distorsions du dessin des barres. Avec une imprimante laser il n'y a aucun problème.

Il semble qu'il n'y ait pas de police gratuite pour codes barre QRcode sur le net. La police utilisée pour les codes Datamatrix peux parfaitement convenir. Elle se compose de 16 combinaisons assignées aux 16 premières lettres majuscules.
Si nous donnons une valeur à chaque point de cette matrice de 2 X 2 comme ceci :

1 2

4 8

la valeur ASCII du caractère associé à une matrice donnée est la somme des valeurs de chaque point + 65 (65 = A = pas de point !)
La police " datamatrix.ttf " (Convient aux QRcodes)
Cette police contient les 16 caractères A (ASCII : 65) à P (ASCII : 80)

Copiez ce fichier
dans le répertoire des
polices, le plus souvent :
C:\WINDOWS\FONTS

Encodage d'un QRcode
Le programme devra se dérouler en plusieurs étapes :

Compactage des données dans les MCs en utilisant les différents modes et en essayant d'optimiser, et si nécessaire ajout du bourrage.

Détermination de la version (Taille) du code.

Placement de tous les modules de fonction (Sauf informations de format).

Découpage en blocs si nécessaire puis calcul des MCs de correction en fonction de la version et du niveau de correction choisi.

Placement des MCs dans la matrice.

Application des différents masques et choix de celui-ci après évaluation des résultats.

Calcul et placement des informations de format.

Transformation de chaque paire de ligne en chaine de caractère. La longueur de la chaine est : nombre de modules / 2. Le nombre de ligne (ou colonne) étant impair, on ajoutera à droite et en bas une ligne de modules blancs.

Du fait de l'interaction entre les différents modes de compression il est difficile de faire une optimisation à 100%. La norme donne toutefois en annexe J une méthode d'optimisation ...
L'évaluation du résultat des différents masque se fera "à l'oeil" et par test des codes obtenus.
Un petit programme pour tester tout ça

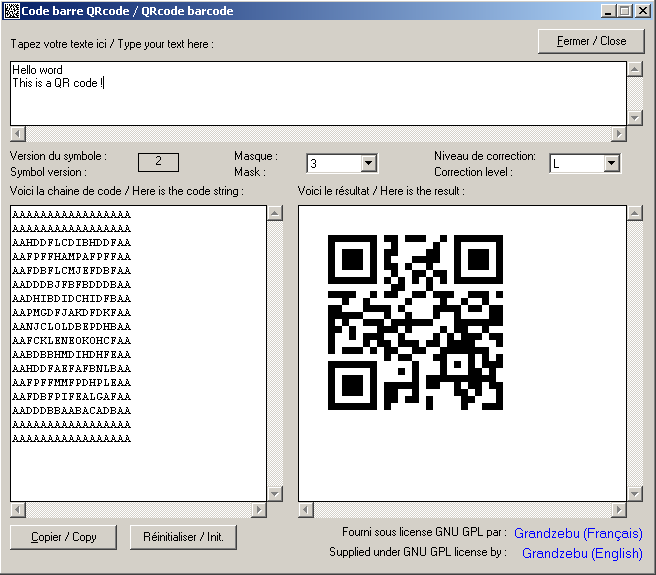
TRAVAIL EN COURS

La fonction QRcode$ fait environ 900 lignes, je ne la reproduis donc pas ici, il suffit de la récuperer dans le fichier "form1.frm" qui se trouve avec le programme ci-dessus ; avec le programme d'auto-installation le fichier "form1.frm" se trouve dans le répertoire du programme, sous-répertoire "sources". La fonction s'appelle de la manière suivante :
resultat$ = QRcode$(Chaine$, Level%, Mask%, Version%, CodeErr%) avec Chaine$ qui doit contenir la chaine à coder, Level% pour le niveau de correction, Mask% pour le masque à utiliser. Au retour Version% donnera la version de code (taille) utilisée et CodeErr% un éventuel numéro d'erreur. Ces deux derniers paramètres sont optionnels et sont passés par références.
Valeurs de CodeErr% au retour de la fonction :
1 : Chaine$ est vide
2 : Chaine$ contient trop de données.
Il suffit maintenant d'afficher ou d'imprimer la chaine resultat$ avec la police Datamatrix par exemple dans un traitement de texte. Les utilisateurs de Word pourront même intégrer la fonction QRcode$ dans une macro afin d'automatiser le traitement. Pour arriver à effectuer tous les traitements dans une unique fonction, j'ai dû utiliser des "Gosub" au lieu de fonctions avec paramètres; j'entends déjà les esthètes de la programmation hurler au sacrilège.

Vous aimez cette page ?

Elle vous est utile ?

Cliquez ici !

Index des mots-clés

Le QR Code

La structure générale.

L'encodage de bas niveau.

L'encodage de haut niveau

La détection et la correction des erreurs.

La création des codes barres.

La police " datamatrix.ttf " (Convient aux QRcodes)

Encodage d'un QRcode

Un petit programme pour tester tout ça

Cliquez ici !

Numéro de masque	Condition
000	(i + j) MOD 2 = 0
001	i MOD 2 = 0
010	j MOD 3 = 0
011	(i + j) MOD 3 = 0
100	((i DIV 2) + (j DIV 3)) MOD 2 = 0
101	(i j) MOD 2 + (i j) MOD 3 = 0
110	((i j) MOD 2 + (i j) MOD 3) MOD 2 = 0
111	((i + j) MOD 2 + (i j) MOD 3) MOD 2 = 0

Mode de compression	Données à encoder	Taux de compression	Indicateur de mode
Numérique	Chiffres ASCII	3 chiffres dans 10 bits	0001
Alphanumérique	Chiffres + lettres majuscules + 9 symboles	2 caractéres dans 11 bits	0010
Octet	Octet	1 octet dans 8 bits	0100
Kanji	Caractères asiatiques	/	1000

Valeur	Caractère	Valeur	Caractère	Valeur	Caractère	Valeur	Caractère
0	0	13	D	26	Q	39	*
1	1	14	E	27	R	40	+
2	2	15	F	28	S	41	-
3	3	16	G	29	T	42	.
4	4	17	H	30	U	43	/
5	5	18	I	31	V	44	:
6	6	19	J	32	W
7	7	20	K	33	X
8	8	21	L	34	Y
9	9	22	M	35	Z
10	A	23	N	36	(Espace)
11	B	24	O	37	$
12	C	25	P	38	%