The PDF417 code

This code is part of the family of 2-dimensional codes, it's in fact a code of several lines which can encode up to 2700 bytes what explain its name "Portable Document File". The encoding is done in two stages : first the datas are converted into "codeword" (High level encoding) then those are converted to bars and spaces patterns. (Low level encoding) In addition, a multi-level error correction system is included, it allows to reconstruct badly printed, erased, fuzzy or torn off datas. In the remainder of this presentation, the expression "codeword" will be shortened to CW and "Reed-Solomon code" to RS.

The general structure.

The width of the finest bar is called the module.
Thereafter a bar module is symbolized by "1" and a space module by "0".
The code consists of 3 to 90 rows.
A line is composed of 1 to 30 columns of datas and its width goes from 90 to 583 modules with the margins.
Maximum number of CW per bar codes : 928 including 925 for datas. (1 for the length descriptor and 2 at least for the correction of errors.)
If necessary a mechanism called "Macro PDF417" allows to distribute more datas on several bar codes.
There are 929 CW including 900 for the datas, they are numbered from 0 to 928.
The errors correction levels goes from 0 to 8. The correction comprises 2 (on level 0) to 512 (on level 8) RS.
The row consists of a start character, a left side CW, 1 to 30 CW of datas, a right side CW and a stop character. There must be a white margin of at least 2 modules on each side.
Filling MCs (We will use for example "900") can be inserted between the data MCs and the correction RS, these must be at the end.
The first MC indicates the total number of MCs of the code including the datas, the filling MCs and itself but excluding the correction RSs.
Example of a code with 14 MC of data, a 15th MC to indicate the total, one filling MC and 4 correction RS. (Level 1)

D é b u t	G1	D15	D14	Dr1	F i n
	G2	D13	D12	Dr2
	G3	D11	D10	Dr3
	G4	D9	D8	Dr4
	G5	D7	D6	Dr5
	G6	D5	D4	Dr6
	G7	D3	D2	Dr7
	G8	D1	D0	Dr8
	G9	C3	C2	Dr9
	G10	C1	C0	Dr10

D15 = length descriptor (16 in this sample)
D0 = padding
D1 to D14 = datas
G1 to G10 = left side CW
Dr1 to Dr10 = right side CW
C0 to C3 = error correction, level 1

Low level encoding.

Each CW is made of 17 modules, containing 4 bars and 4 spaces (Code name comes from there !) and it start by a bar. Bars and spaces width is 1 to 6 modules. (Except for start and stop characters) Sample :

soit la formulation suivante : 111 0 1 0 1 000 111 0000
Start character is : 11111111 0 1 0 1 0 1 000
Stop character is : 1111111 0 1 000 1 0 1 00 1 (Here there is a 5th bar, thus 18 modules.)
There are 3 distinct tables for encoding the 929 CW.
The 3 tables giving the patterns of the 929 MC begin like this :

First table	Second table	Third table	Exhaustive tables file :
111 0 1 0 1 0 111 000000	11111 0 1 0 1 0 11 00000	11 0 1 0 1 0 11111 00000
1111 0 1 0 1 0 1111 0000	111111 0 1 0 1 0 111 000	111 0 1 0 1 0 111111 000
11111 0 1 0 1 0 11111 00	1111 0 1 0 1 00 1 000000	1 0 1 0 1 00 1111 000000
111 0 1 0 1 00 111 00000	11111 0 1 0 1 00 11 0000	11 0 1 0 1 00 11111 0000
.....	.....	.....

Each row use only one encoding table, this table will be used again 3 rows further. Sample : Row 1 --> table 1, row 2 --> table 2, row 3 --> table 3, row 4 --> table 1, .....etc. We have the formula : table number = ( ( row number MOD 3 ) * 3 )

High level encoding.

Thereafter we'll use operators : + --> addition, x --> multiplication, \ --> integer division, MOD --> remainder of the integer division.
Datas are compacted into CW according to 3 modes which are conceived according to their efficience compared to the datas type. Default mode is "Text" mode.

Compaction mode	Datas to encode	Rate compaction
"Byte"	ASCII 0 to 255	1,2 byte per CW
"Text"	ASCII 9, 10, 13 & 32 to 127	2 characters per CW
"Numeric"	Only digits 0 to 9	2.9 digits per CW

CWs numbered 900 to 928 have a special meaning, some allow switching from one mode to another in order to optimize the code.

CW number :	Function
900	Switch to "Text" mode
901	Switch to "Byte" mode
902	Switch to "Numeric" mode
903 à 912	Reserved
913	Switch to "Byte" only for the next CW
914 à 920	Reserved
921	Initialization
922	Block termination for PDF macro
923	Field identification sequence in a PDF macro
924	Switch to "Byte" mode (If number of bytes multiple of 6)
925	ECI custom identifier
926	ECI general identifier
927	ECI identifier for character set or code page
928	Block start for PDF macro

The "Text mode have 4 sub-modes :

Uppercase
Lowercase
Mixed : Numeric and punctuation
Punctuation

The default sub-mode is "Uppercase", in this sub-mode 2 characters are encoded in each CW, here is characters tables :

Value	Uppercase	Lowercase	Mixed	Punctuation
0	A	a	0	;
1	B	b	1	<
2	C	c	2	>
3	D	d	3	@
4	E	e	4	[
5	F	f	5	\
6	G	g	6	]
7	H	h	7	_
8	I	i	8	` (Quote)
9	J	j	9	~
10	K	k	&	!
11	L	l	CR	CR
12	M	m	HT	HT
13	N	n	,	,
14	O	o	:	:
15	P	p	#	LF
16	Q	q	-	-
17	R	r	.	.
18	S	s	$	$
19	T	t	/	/
20	U	u	+	“
21	V	v	%	\|
22	W	w	*	*
23	X	x	=	(
24	Y	y	^	)
25	Z	z	PON	?
26	SP	SP	SP	{
27	MIN	T_MAJ	MIN	}
28	MIX	MIX	MAJ	' (Apostrophe)
29	T_PON	T_PON	T_PON	MAJ

6 switchs are included in these tables, they allow to change the sub-mode :
UPP : switch to "Uppercase"
LOW : switch to "Lowercase"
MIX : switch to "Mixed"
PUN : switch to "Punctuation"
T_UPP : switch to "Uppercase" only for next character
T_PUN : switch to "Punctuation" only for next character
Each CW encode 2 characters ; if C₁ and C₂ are the values of the two characters, CW value is : C₁ x 30 + C₂
If it remains an alone character, we add to it a padding switch, for instance T_PUN.

Sample, sequence to encode : Super !

S : 18, LOW : 27, u : 20, p : 15, e : 4, r : 17, SPACE : 26, T_PUN : 29, ! : 10
that is 9 characters, we'll add a T_PUN for the padding.
CW₁ = 18 x 30 + 27 = 567
CW₂ = 20 x 30 + 15 = 615
CW₃ = 4 x 30 + 17 = 137
CW₄ = 26 * 30 + 29 = 809
CW₅ = 10 x 30 + 29 = 329
The sequence is consequently : 567, 615, 137, 809, 329

The "Byte" mode allow to encode 256 different bytes, that is the entire extended ASCII table.
If the byte number is a multiple of 6, we use the CW numbered 924 to switch to "Byte" mode; if the byte number is not a multiple of 9 we use the CW numbered 901 for switching.
Coding consists has to transform 6 bytes in base 256 to 5 CW in base 900. To carry out the conversion :

Take the bytes by group of 6; let X₅ to X₀ their decimal values. (X₀ is the less significantcharacter)
Compute the sum S = X₅ x 256⁵ + X₄ x 256⁴ + X₃ x 256³ + X₂ x 256² + X₁ x 256 + X₀
Let's compute the CWs : CW₀ = S MOD 900, new value of S : S = S \ 900, CW₁ = S MOD 900 ... and so forth to CW4 (CW₀ is the less significant CW)
Bytes which remains after the conversion of the groups of 6 are taken just as they are : 1 byte = 1 CW of same value.

Sample 1 : word to encode : alcool

The sequence of bytes (in ASCII) is : 97, 108, 99, 111, 111, 108
S = 97 x 256⁵ + 108 x 256⁴ + 99 x 256³ + 111 x 256² + 111 x 256 + 108 = 107 118 152 609 644
CW₀ = 107 118 152 609 644 MOD 900 = 244
S = 107 118 152 609 644 \ 900 = 119 020 169 566
CW₁ = 119 020 169 566 MOD 900 = 766
S = 119 020 169 566 \ 900 = 132 244 632
CW₂ = 132 244 632 MOD 900 = 432
S = 132 244 632 \ 900 = 146 938
CW3 = 146 938 MOD 900 = 238
S = 146 938 \ 900 = 163
CW4 = 163 MOD 900 = 163
The sequence including the switch is consequently : 924, 163, 238, 432, 766, 244

Sample 2 : word to encode : alcoolique

The sequence of bytes (in ASCII) is : 97, 108, 99, 111, 111, 108, 105, 113, 117, 101
The first 6 bytes are coded like above and we add 105, 113, 117 and 101
The sequence including the switch is consequently : 901, 163, 238, 432, 766, 244, 105, 113, 117, 101

The "Numeric" mode is a conversion from base 10 to base 900
To carry out this conversion :

Take the digits by group of 44 (or less for the rest)
Add the digit 1 ahead, it will be removed by the decoding procedure
Make the change of base like for the "Byte" mode
Each group of 44 digits give 15 CWs
The smallest groups give a number of CW witch is : Number of digits \ 3 + 1
Sample : 10 digits give 10 \ 3 + 1 = 3 + 1 = 4 CWs

Sample, sequence to encode : 01234

There will be thus 5 \ 3 + 1 = 2 CW
Add a "1" ahead : 101234
CW₀ = 101 234 MOD 900 = 434
S = 101 234 \ 900 = 112
CW₁ = 112 MOD 900 = 112
The sequence is consequently : 112, 434

Left and right side CWs are computed according to the table used for the current row.
To obtain the CW value, make the following calculation : (Row Number \ 3) x 30 + X with X taken in the following table. (First row is row number 0)

Table used to encode the CWs of this row	X for the left side CW	X for the right side CW
1	(Number of rows -1) \ 3	Number of data columns - 1
2	(Security level x 3) + (Number of rows -1) MOD 3	(Number of rows -1) \ 3
3	Number of data columns - 1	(Security level x 3) + (Number of rows -1) MOD 3

Errors detection and correction.

Error detection system use 2 CWs and correction system use some between 2 and 510
The correction system is based on " Reed Solomon codes " which enjoy the math students and terrify others ...
Number of CWs to add depend of the correction level used, because of the limit to 928 CWs in a bar code (1 of which for the sum of CWs) the maximum level is limited by the number of data CWs. The number of CWs that the error correction algorithm can reconstitute is equal to the number of CWs required by the correction system : this is not magic but it's mathematical !

Level	Number of CWs required by the correction system, 2 of which for the detection ( 2^{level + 1})	Maximum number of data CWs
0	2	925
1	4	923
2	8	919
3	16	911
4	32	895
5	64	863
6	128	799
7	256	671
8	512	415

The advisable correction level depend on the number of data CWs :

Number of data CWs	Advisable level
1 à 40	2
41 à 160	3
161 à 320	4
321 à 863	5

Reed Solomon codes are based on a polynomial equation where x power is 2^s+1 with s = error correction level used. For sample with the level 1 we use an equation like this : a + bx + cx² + dx³ + x⁴ The numbers a, b, c and d are the factors of the polynomial equation.
For information the equation is : (x - 3)(x - 3²)(x - 3³).....(x - 3^k) ( with k = 2^s+1) We develop the polynomial equation and we apply a MOD 929 on each factor. These factors have been pre-computed for the 8 equations corresponding to the 8 correction levels. You can see the factors file. We can also calculate them.

Here in Basic the algorithm to calculate the coefficients :

Let s the correction level used, k = 2^s+1 the number of RS.
Now, still in Basic, the algorithm for calculating RS codes.

Find all the RS code calculations of the different 2D barcodes in Visual Basic 6.
It is a ZIP file without installation :

Those who have read and understood the codes of Reed Solomon will find themselves there ; for the few ignorant who have not understood everything (like me!) It will be enough to apply the "recipe" by using the codes obtained in the reverse order (last to first).

Bar code making.

Since we can create the bar code pattern it remains us to draw it on the screen and to print it on a paper sheet. Two approaches are possible :

The graphic method where each bar is "drawn" like a solid rectangle. This method makes it possible to calculate the width of each bar to the nearest pixel and to work on multiples of the width of a pixel of the used device. This gives good accuracy especially if the device has a low density as is the case of screens and inkjet printers. This method require special programming routines and does not allow to make bar codes with a current software.
The special font in which each character is replaced by a bar code. This method allow the use of any software like a text processing or a spreadsheet. (For example LibreOffice, the free clone of MSoffice !) The scale settings according to the selected size can bring small misshaping of the bar drawing. With a laser printer there's no probs.

It seems there is no free font for PDF417 on the net. I've decided consequently to draw this font and to propose it for download. Because there's 929 CWs with 3 alternatives for each one obligate us to divide the 17 bits of a CW in several parts. But divide by 17 ... hmmm ... a trick is necessary. If we considere that the first bit is always "1" and the last one "0", we can imagine a separator like "01" and the remain is only 15 bits in each CW; we can then divide these 15 bits into 3 parts. There will be then 2⁵ = 32 possible groups affected to 32 characters of the font. The encoding software is in charge to transform the 3 groups of each CW into a 3 characters string.
The font will contain thus the following characters :

Character A (ASCII : 65) to F (ASCII :70) and a (ASCII : 97) to z (ASCII :122) for the 32 groups having a formula "00000" to "11111"
Character * (ASCII : 42) for the separator having a formula "01"
Character + (ASCII : 43) for the row start character without its last 0, formula "11111111 0 1 0 1 0 1 00"
Character - (ASCII : 45) for the end row character without its first 1, formula "111111 0 1 000 1 0 1 00 1"

The string to send to the printer will look something like this : +*gfA*jhD*BAl*gCt*hjk*- and this for each row.

The "pdf417.ttf" font

This font contains the 35 patterns describe above. The start row and end row codes embed a 2 modules margin. The height is equal to 3 modules which is the most usual size.

Copy this file
in the font directory,
often named :
C:\WINDOWS\FONTS

Encoding a pdf417 bar code

The software will evolve with 4 steps :

Compaction of the datas into the CWs by using of the different methods and trying to optimize.
Calculation of the correction CWs according to the selected security level.
Splitting by rows and addition of left side and right side CWs.
Transformation of each CW into a 3 characters string and addition of separators, start row character, end row character and carriage returns.

Because of the interaction between the different compaction modes and the different sub-modes of the "text" mode it's difficult to make a 100% optimization. Thus the software will split the string into "parts" having the type "numeric", "text" or "byte" afterwards it will change some parts for an other mode if the overload due to switch CWs is greater than the compaction gain. We'll can't make allowance for all the parameters like paddings, gain due to perfect multiple of 6, uni-character switch or the switchs between the different sub-modes of the text mode : one would need for that several thousands of programming lines.
Another difficulty comes from the size of the wielded numbers, for example the "Modulo 900" operation applied on a 44 digits number generate an unavoidable overload error; the software will have to carry out this calculation step by step.

A small program to test all that

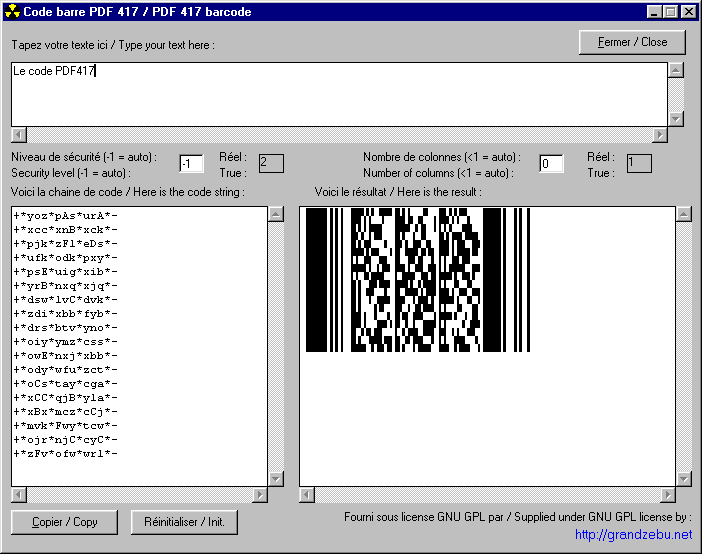
Here is a small program
written with Visual Basic 6.
The setup file copy the
program, the Visual Basic
dependencies, the source
files and the font.

Setup file :

ZIP file without setup :

The PDF417$ function have about 500 lines, I thus don't reproduce it here, you can retrieve it in the "form1.frm" file which is with the above program ; with setup program, the "form1.frm" file is in the program directory, "sources" sub-directory.
The function call is like this : result$ = pdf417$(String$, Security%, ColNb%, ErrCode%)
with the string to encode in String$, correction level in Security% (-1 = auto.), ColNb% for the number of data columns in a row (<1 = auto.) and ErrCode% for retrieving an eventual error code. these 3 last parameters are not required and are passed by references ; after the function return they contains the really used values. Values of ErrCode% after the function return :

1 : String$ is empty
2 : String$ have too many datas, we go beyond the 928 CWs.
3 : Number of CWs per row too small, we go beyond 90 rows.
10 : The security level has being lowers not to exceed the 928 CWs. (It's not an error, only a warning.)

It is enough now to display or to print the chains result$ with the pdf417 font for example in a text processing. The Word users will be able to even integrate the pdf417$ function in a macro to automate the treatment. To achieve all the treatments in a single function, I had to use "Gosub" instead of functions with parameters ; I can already hear the programming esthetes screaming sacrilegious !

Do you like this page ?

Is it useful to you ?

Index des mots-clés